Altra figura luminosa è stata quella di Eratostene di Cirene (276 a.C. – 194 a.C.). Egli aveva avuto notizia (o, forse, lo aveva constatato direttamente) che a Siene (l’odierna Assuan), nell’Alto Egitto, il Sole era esattamente allo zenit il giorno del solstizio estivo. Ciò era provato dal fatto che a mezzodì di quel giorno, entro un raggio di circa mezzo miglio e per un attimo, il fondo di ogni pozzo appariva completamente illuminato dalla luce del Sole. Invece ad Alessandria d’Egitto, nello stesso giorno ed alla stessa ora, gli obelischi e le altre strutture verticali producevano un’ombra, seppure molto corta. Eratostene allora, con geniale intuizione, misurò mediante l’utilissimo gnomone, che ben conosciamo, la lunghezza dell’ombra a mezzogiorno del solstizio d’estate ad Alessandria e riuscì facilmente a calcolare l’angolo tra la direzione del Sole e quella della verticale del luogo (ossia quella dello gnomone), come riportato nella figura che segue
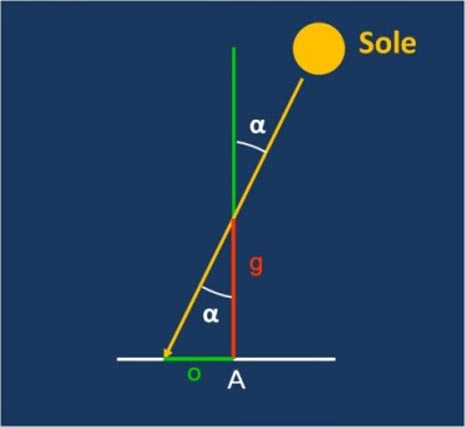
Eratostene misurò il rapporto tra la lunghezza dell’ombra o e l’altezza dello gnomone g e calcolò facilmente l’angolo α tra la verticale del luogo e la direzione del Sole. In trigonometria vale la relazione tan(α) = o/g e quindi α = arctan(o/g).
Aveva già mandato nel frattempo il suo servo a Siene a dorso di dromedario per misurare il più esattamente possibile la distanza tra le due città. A quei tempi le misure venivano fatte in “ore” o “giorni” di dromedario … A questo punto Eratostene fece una semplice proporzione e calcolò la misura della circonferenza terrestre come illustra la figura
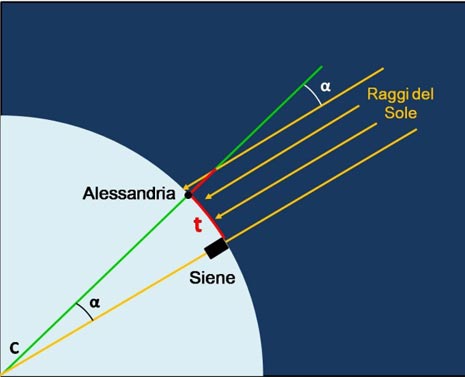
Con il suo gnomone Eratostene misurò l’angolo α tra la direzione del Sole e la verticale CA. ma dato che allo stesso istante a Siene la luce del Sole arrivava perfettamente verticale, concluse che α era anche l’angolo tra Alessandria e Siene viste dal centro della Terra. t era stato misurato con il dromedario e quindi egli impose la semplice proporzione t: α = circonferenza terrestre: 360°. Tutto era conosciuto tranne la circonferenza terrestre che risultò sbagliata di meno del 2% rispetto al valore reale!! Sicuramente Eratostene era geniale, ma anche il suo dromedario era un ottimo camminatore!
In pratica l’angolo misurato ad Alessandria con lo gnomone doveva essere era lo stesso tra Alessandria e Siene viste dal centro della Terra. Notiamo che il ragionamento era valido soprattutto a seguito della importante assunzione che i raggi solari potessero essere considerati paralleli tra loro, ossia che il Sole si trovasse a distanza enorme rispetto alle dimensioni della Terra. Era inoltre necessario che Alessandria e Siene fossero sullo stesso meridiano e questo era praticamente esatto. Eratostene misurò un angolo di 1/50 di circonferenza ed ottenne una distanza tra le due città di 5000 stadi. La semplice proporzione che deriva dalla figura precedente gli permise di calcolare una circonferenza di 250000 stadi, pari a 39375 km, contro gli effettivi 40000. Grande Eratostene ma perfetto come contachilometri anche il dromedario!
Eratostene eseguì anche misure delle distanze del Sole e della Luna, ottenendo valori pregevolissimi, indicativi dei progressi nella strumentazione: per il Sole calcolò la distanza di 804.000.000 stadi (all’incirca 130.000.000 Km) e per la Luna 780.000 stadi (all’incirca 125.000 Km). Ottenne questi risultati elaborando dati misurati durante eclissi di Luna. Probabilmente calcolò anche un valore per l’obliquità dell’eclittica di 23° 51’, altro valore estremamente preciso per i suoi tempi.

Interessante… 😉