Le coordinate sferiche, dette anche coordinate polari nello spazio, servono ad identificare un punto preciso nello spazio a tre dimensioni. Se ci chiedessero di descrivere geometricamente la tecnica per identificare un oggetto nel mondo reale, come ad esempio un grosso albero su una collina, come lo faremmo?
Beh, sicuramente utilizzeremmo le dimensioni a noi più note, ovvero altezza, lunghezza e profondità, e con carta e penna cercheremmo di rappresentare il tutto con un grafico. E, forse, il risultato sarebbe simile al seguente:

Ebbene, abbiamo appena utilizzato lo spazio euclideo, e un “sistema” di coordinate. Sistema che, come tutti gli altri che vedremo nel corso della guida, appartiene proprio ai già citati sistemi di coordinate sferiche. Essi identificano un punto nello spazio una volta fissata una terna di assi cartesiani (x ,y, z).
Descrivendo quanto appena detto dal punto di vista geometrico, un punto generico S è individuato dalla terna di parametri ρ (Rho), θ (Theta) e φ (Phi) in cui:
ρ è il cosiddetto raggio vettore (distanza dal punto di origine del sistema O), ovvero il segmento OS che ha come punto iniziale l’origine del sistema O e come punto d’arrivo il nostro ipotetico oggetto S. In pratica, questa è la distanza che ci separa dal nostro oggetto osservato.
l’angolo φ si definisce distanza zenitale o colatitudine, ovvero l’angolo formato da OS con l’asse z.
l’angolo θ prende il nome di azimut o longitudine, ed è l’angolo formato da OV con l’asse x, dove V è la proiezione ortogonale (perpendicolare) del punto S sul piano xy.
I sistemi di coordinate sferiche si basano quindi su tre parametri, detti riferimenti fondamentali: una direzione fondamentale, ovvero l’asse polare “z” passante per l’origine del sistema. Un piano fondamentale (xy) perpendicolare a tale direzione e passante anch’esso per l’origine. Una distanza (ρ) dal punto di origine del sistema, chiamato raggio vettore.
Tuttavia, dobbiamo ricordare che quando parliamo di coordinate, siano esse astronomiche o geografiche, il raggio vettore (ρ) è irrilevante, in quanto, per convenzione, la sfera celeste viene vista come una superficie curva a due dimensioni, proprio come la superficie terrestre. Ecco quindi che nei sistemi di coordinate che andremo a conoscere saranno necessari solo due riferimenti fondamentali, perpendicolari tra loro: una direzione e un piano.
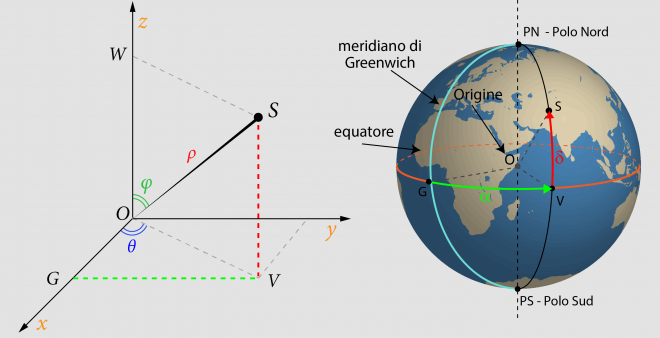
Una volta fissato bene questo concetto possiamo provare a trasporre sulla sfera terrestre il sistema di coordinate rappresentate nel grafico. Mettendo a confronto le due figure qui sopra troveremo che:
- al centro del sistema O c’è il centro della Terra
- quello che a sinistra è l’asse z, sulla sfera terrestre individua la direzione fondamentale, ovvero l’asse terrestre (che quindi identificherà il Polo Nord!), ma ricordiamo che in un altro sistema di coordinate la direzione potrebbe passare per punti diversi della sfera celeste, a seconda dei riferimenti scelti
- il piano delimitato da x e y è quello che passa per il piano fondamentale, che sulla Terra (e sul suo unico sistema di coordinate) coincide con l’equatore.
- l’angolo φ chiamato distanza zenitale o colatitudine, che ci permette di calcolare, per differenza, la latitudine e cioè il segmento d (delta) che va dal punto V sull’equatore al punto S, lungo il meridiano passante per S
- infine troviamo θ chiamato azimut o longitudine, che sulla sfera altro non è che il segmento α (alfa) che seguendo il piano fondamentale va dal punto G al punto V, e cioè dall’intersezione tra il meridiano fondamentale di Greenwich (che descriveremo nel successivo appuntamento) e l’equatore, all’intersezione del meridiano passante per S con il piano fondamentale (equatore)
Ma come facciamo a identificare un punto su una superficie sferica una volta conosciuti i riferimenti fondamentali? Ci sono dei punti presi per convenzione da cui iniziare a “prendere le misure”? Una piccola parte del quesito è stata già anticipata introducendo il concetto di meridiano, ma avremo un quadro più completo leggendo il capitolo che segue.
