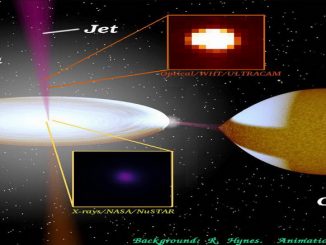
Questi fenomeni prendono il nome di sorgenti superluminali, in quanto sembrano propagarsi a velocità di gran lunga superiori a quella della luce. Normalmente sono associati a galassie attive e si formano a causa della caduta di materiale verso il buco nero centrale. Si presentano normalmente come getti di particelle che vengono scagliate verso lo spazio. Al loro interno si notano nodi più densi che permettono di misurarne la velocità, dato che sono segni particolari che possono essere seguiti col telescopio durante un periodo relativamente breve. Misurando lo spazio percorso da questi nell’unità di tempo si determina la velocità del getto. Molte volte essa appare ben superiore alla velocità della luce, da cui il nome di sorgenti superluminali.
Come vi dicevo fin dall’inizio questi valori assurdi per la fisica odierna derivano da un fenomeno prospettico non molto facile da descrivere. Per farne una trattazione precisa e quantitativa dovrei introdurre parecchie formule trigonometriche e approssimazioni non sempre intuitive. Insomma, renderei le cose comprensibili solo a un numero probabilmente limitato di lettori. Non ho in realtà trovato testi che riescano a semplificare più di tanto la problematica e allora ci provo da solo, sperando di non commettere errori troppo grossolani. Come vi ho detto spesso, l’importante è capire i concetti e non imparare mnemonicamente una serie di nozioni.
Consideriamo allora la Fig.1 in cui S1 sia la sorgente del getto. Ammettiamo per adesso che la direzione del getto avvenga esattamente in direzione trasversale rispetto all’osservatore. Al tempo t1’ osservo la luce del nodo partita al tempo t1 (la differenza tra questi tempi dipende ovviamente dalla distanza della sorgente da noi e potrebbe anche essere di miliardi di anni, ma a noi poco importa). Al tempo t2 il nodo si sarà spostato in S2 e la sua luce giunge sulla Terra al tempo t2’. Per percorrere il tratto S1S2 = d nel tempo t2 – t1 il nodo ha viaggiato al velocità v = d/(t2 – t1). Questa è la velocità reale del getto e non può ovviamente superare quella della luce. Tuttavia, le si avvicina molto e questo è estremamente importante.
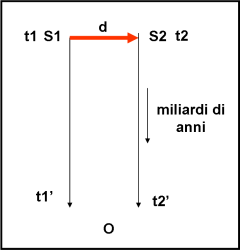
L’osservatore misura, ovviamente, la differenza di tempo (t2’- t1’) e la distanza d. Per la situazione rappresentata nella Fig. 1, la differenza t2’ – t1’ risulta perfettamente uguale a quella t2 – t1. Notate che per i valori estremamente piccoli dell’intervallo di tempo e della distanza percorsa posso trascurare completamente gli effetti dovuti all’espansione dell’Universo (lo Spazio si espande ma non i singoli oggetti e qui il getto può considerarsi come un singolo oggetto).
Se vado a calcolare la velocità osservata da Terra devo fare v’ = d/(t2’- t1’), che però è anche uguale a v = d/(t2 – t1), dato che t2 – t1 = t2’- t1’. La velocità misurata è altissima ma non va contro la teoria della relatività.
Non siamo, pero, sempre così fortunati… Consideriamo la Fig. 2, dove il getto è inclinato e forma un angolo a, abbastanza piccolo, con la linea di vista. Noi, ovviamente non possiamo sapere la configurazione effettiva della sorgente e del suo getto e dobbiamo limitarci a eseguire i calcoli basandoci su quello che vediamo, che, in questo caso, è una proiezione di quanto capita realmente sulla sfera celeste. Possiamo, oltretutto, calcolare solo i tempi di arrivo sulla Terra della luce del nodo durante il suo percorso.

La distanza d sarà esattamente uguale a quella precedente (anche se non possiamo sapere se è una proiezione o quella effettiva). Misuriamo nuovamente la differenza osservata tra i tempi t2’ e t1’. Con grande meraviglia troveremo che v = d/(t2’– t1’) supera di gran lunga la velocità della luce. Dov’è l’errore?
State bene attenti… il calcolo che abbiamo fatto ora presuppone che le condizioni effettive siano come quelle del caso fortunato della Fig.1. D’altra parte, da terra, non possiamo fare altro. Siamo, quindi, costretti a considerare t2’– t1’ uguale a t2 – t1, ossia a considerare la differenza di tempo tra S2 e S1 come nel caso precedente. E qui commettiamo l’errore fondamentale. La differenza effettiva di tempo tra gli eventi REALI S2 e S1 è ben maggiore di t2’ – t1’. Infatti, la luce che è arrivata da noi al tempo t1’, relativa alla sorgente in S1, è partita ben prima (t0) di quanto rappresentato in Fig. 1. Essa ha dovuto percorrere un tratto decisamente più lungo rispetto a quella che ha percorso S2. Per trovare la vera velocità del getto dovremmo dividere la distanza per un tempo molto più lungo (che non possiamo conoscere). E invece dividiamo per un valore più piccolo, che relativamente a quello vero decresce col decrescere dell’angolo a. Dividendo una distanza costante per un tempo sempre più corto rispetto a quello effettivo, troviamo una velocità sempre più grande che può tranquillamente superare di molto quella della luce, dato che la velocità reale è solo di poco inferiore.
Vi sono molti modi per spiegare e per quantificare questo effetto, ma tutti fanno uso di formule più o meno complicate. Sono riuscito a non usarne nessuna (tranne la definizione di velocità, ma… quella DEVE essere patrimonio dell’umanità astronomia.comiana intera!). Adesso spero solo che questo tentativo sia servito a far comprendere il concetto base Se vi sono dubbi o suggerimenti, sparate pure! Insieme, possiamo migliorare ancora l’esposizione…



Direi che il concetto generale è spiegato bene e almeno per me è abbastanza chiaro, l'unico dubbio che mi rimane è che nella figura 2 l'oggetto al tempo t2 si trova più vicino all'osservatore rispetto alla posizione al tempo t1, ma se l'universo si espande non dovrebbe risultare più lontano?
non confondiamo pomodori con arance... L'espansione dell'universo avviene su larga scala e tutti ne sono influenzati. ma si rende evidente solo per distazne enormi. Qui stiamo parlando di getti e di distanze estremamente piccole, ossia di movimenti propri nello spazio. Anche la Luna si avvicina alla Terra e anche un tuo amico per strada. però non pensi all'espansione dell'Universo che dovrebbe allontanarvi sempre di più. I movimenti tra oggetti celesti (pianeti, stelle, galassie, ammassi di gallasie) continuano ad esistere in tutte le direzioni dello spazio. E' poi lo spazio che si allarga sempre più, ma non influisce più di tanto sui movimenti.
locali... Anche Andromeda si scontrerà con la Terra, ma esse sono così vicine che questo movimento non viene influenzato dall'espansione dello spazio.
Penso che ti farebbe bene una lettura del libro, proprio per comprendere bene le differenze e le relazioni tra i moti del teatro del Cosmo...
Va bene è tutto chiaro, questa differenza nei movimenti reciproci che hai spiegato la conoscevo, avevo interpretato male il "miliardi di anni" sulla figura, avevo pensato a un ordine di grandezza più alto rispetto a quello che in realtà è, quindi ho partorito questa domanda un po' stupida nel senso che ragionandoci meglio avrei potuto evitarla, grazie comunque per il chiarimento.
Grazie per l'articolo Enzo. ...darei un braccio per sapere quali reazioni si susseguono all'interno di questi getti! E' mai stato studiato che effetti possano scatenare a livello di campi gravitazionali?
...darei un braccio per sapere quali reazioni si susseguono all'interno di questi getti! E' mai stato studiato che effetti possano scatenare a livello di campi gravitazionali?
Beh, gia il fatto che possiamo vederlo dovrebbe essere un chiaro indizio che qualcosa non quadra....quello che mi fa impressione é l'immaginare che razza di energia sia necessaria per muovere della materia(si sa che particelle sono?) a tali velocità
In effetti sembra quasi paradossale, visto che nella vita di tutti i giorni succede praticamente l'esatto opposto! (Osservando un oggetto in movimento "di sbieco" appare muoversi più lentamente che nella realtà).

Per comprenderlo appieno ho dovuto figurarmi dove si trovino al tempo t2 i "raggi lumnosi" partiti in t1 nella prima figura e in t0 nella seconda.
A quel punto diventa immediatamente chiaro, anche "a occhio", che la differenza t2'-t1' nella seconda figura è inferiore rispetto alla prima!
Bella spiegazione! Il getto relativistico che proviene dal grande buco nero distante miliardi di anni luce è un fenomeno a dir poco impressionante, mi immagino lo stupore degli astronomi che per primi hanno osservato con gli strumenti questi fenomeni. La velocità del getto nella figura 2, appare più veloce della luce all'osservatore perché il tratto che percorre è assai più lungo anche se in prospettiva appare lungo uguale al getto della figura 1. In pratica nella figura 2 corrisponde all'ipotenusa di un triangolo rettangolo, mentre il getto nella figura 1 è soltanto un cateto. Le diverse distanze appaiono percorse nello stesso tempo per effetto della prospettiva, quindi la velocità nella figura 1 è reale, quella nella figura 2 superiore a quella della luce è soltanto prospettica, non reale. Mi scuso per le molte parole con cui ha cercato di spiegarmi.
in effetti é controintuitivo pensare che al diminuire dell'angolo a la velocitá (apparente) aumenti, ma se si tiene a mente che la velocitá della luce é costante e che quindi i tempi in cui ci giungono le informazioni di S1 e S2 sono relativi, allora diventa chiaro. o almeno abbastanza :-).
mi sorge peró una domanda: mi pare di aver capito che di questi getti non si conosce l'inclinazione rispetto alla nostra visuale, se siano trasversali o perpendicolari e via dicendo. ma non sarebbe possibile scoprirlo andando a misurare i rispettivi redschift nei punti S1 e S2 per confrontarli e vedere se uno si allontana piú velocemente dell'altro? é forse perché la scala del fenomeno é troppo piccola?
grazie
Il moto proprio di sorgente e osservatore e' trascurabile come lo e' l'espansione dell'universo?
Quello che intendo dire e' che nel momento t1 la distanza tra sorgente e osservatore e' ad esempio k1 (chiamiamola cosi'). Quando eseguo pero' la misurazione nel momento t2 la distanza tra sorgente e osservatore sara' invece k2 (che presumo sara' maggiore di k1 in quanto si parla di oggetti lontanissimi) quindi la distanza d misurata in t2 andrebbe corretta di un valore k2 - k1 giusto?
Questo valore k2 - k1 e' trascurabile?
Temo che tu faccia lo stesso errore che faceva Danilo. Non dovete cercare di capire che la velocià è realmente più veloce della luce, ma solo che è un'apparenza dovuta alla prospettiva della situazione reale che non conosco.