Raccogliere la luce non è cosa facile

Accettato il fatto che contro la diffrazione non vi è niente da fare, vediamo ora i tipi di obiettivo che sono normalmente utilizzati nelle osservazioni astronomiche. Vi sono solo due fenomeni capaci di deviare un raggio luminoso dal suo percorso rettilineo: la rifrazione e la riflessione. E’ ovvio, quindi, che un obiettivo, il cui scopo è proprio quello di fare convergere raggi tra loro paralleli, debba sfruttare uno di loro. In realtà, anche la gravità riesce a ottenere lo stesso risultato, ma l’uomo deve andare a cercare la “lente” tra quelle già costruite dell’Universo e non può certo elaborarla per i propri scopi. Possiamo quindi tralasciare la lente gravitazionale tanto utile per lo studio delle galassie più lontane. Non possiamo nemmeno pensare di utilizzare laghi e laghetti che il nostro amico pescatore conosce molto bene. Meglio dedicarsi al vetro, all’argento, all’alluminio e a sostanze più moderne e attraenti.

Per far ciò prendiamo due oggetti molto comuni nella vita di tutti i giorni; una lastra di vetro e uno specchio. Cosa riescono a fare se inseriti lungo il percorso della luce che proviene da una stella? Lo vediamo nella Fig. 1, anche se ormai dovremmo saperlo molto bene.

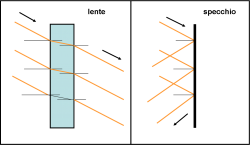
E’ necessario curvare

Una lastra di vetro di un certo spessore devia il raggio luminoso avvicinandolo alla normale alla superficie di contatto tra aria e vetro, ma, poi, è costretta a farlo di nuovo allontanare in modo esattamente uguale e contrario a quanto fatto all’entrata, quando la luce esce nuovamente allo scoperto. Conclusione? I raggi si sono spostati leggermente ma sono rimasti paralleli tra loro. Sappiamo che succede anche qualcos’altro (prisma o goccia d’acqua), ma per adesso tralasciamolo. Proviamo, adesso, a inserire lo specchio. Il raggio torna nella direzione da cui è venuto formando un angolo uguale a quello di incidenza tra lui e la normale alla superficie. Anche questo fenomeno lo conosciamo molto bene, ma, ancora una volta, i raggi restano paralleli anche se deviano nettamente il loro percorso primitivo. Ogni raggio del fascio segue perfettamente ciò che fanno i compagni di viaggio.

Dobbiamo, perciò, concludere che la superficie da interporre al raggio di luce deve essere curvilinea per sperare che ogni raggio segua un percorso diverso da quello dei fratelli paralleli. Scusate se la trattazione può sembrare banale e quasi infantile, ma è sempre importante avere le idee chiare fin dall’inizio. Una curva ha in ogni suo punto una perpendicolare alla tangente, tracciata per quel punto, che differisce da quella del compagno vicino. Non abbiamo ancora risolto niente, ma, almeno, siamo riusciti a deviare i raggi in modo diverso tra loro, dato che sappiamo benissimo che o si rifrangono avvicinandosi alla normale o si riflettono formando un certo angolo con lei.

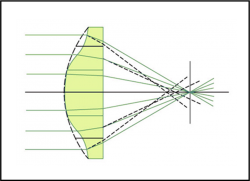
Prendiamo allora il pezzo di vetro a facce piane e parallele e lavoriamo queste ultime in modo che diventino entrambe una porzione di superficie sferica. Abbiamo ottenuto una lente. Se la mettiamo contro i raggi del Sole vediamo che formano un punto molto luminoso su un foglio di carta. Spostando il foglio può anche capitare che prenda fuoco. Evviva! Abbiamo concentrato i raggi luminosi in un punto. La spiegazione “tecnica” ce la mostra la Fig. 2. la rifrazione e le perpendicolari sempre diverse tra loro hanno compiuto il miracolo. L’immagine della stella si è formata in un punto (o quasi, ricordando la diffrazione). Tutto ciò che è stato descritto nell’articolo precedente è diventato realtà.

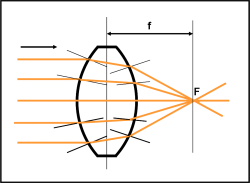
Ovviamente, sorgono dei problemi. Se vogliamo diminuire il disco di Airy dobbiamo aumentare le dimensioni della lente. Il vetro purtroppo pesa e una lente anche. Oltretutto, più è grande la superficie e più difficile è riuscire a farla diventare perfettamente sferica. Non possiamo permetterci di fare un lavoro approssimativo. Tutto deve essere preciso se vogliamo almeno arrivare ai limiti imposti dalla diffrazione. La prova di quanto detto si ha notando che il telescopio a lente più grande del mondo non supera il metro di diametro. Valore enorme per una lente, ma ridicolo se si vuole raccogliere veramente molta luce e spingersi ai confini dell’Universo, raccogliendo anche quella partita miliardi di anni fa.

I colori non sono sempre una gioia

Ci si potrebbe anche accontentare per osservare oggetti vicini, ma sorgerebbe comunque un problema molto evidente che conosciamo bene e che viene sfruttato egregiamente per altri scopi sia dalla tecnica umana che dalla Natura. Quale? Basta ricordare il prisma e l’arcobaleno. Ogni lunghezza d’onda si avvicina o si allontana dalla perpendicolare in modo diverso. La Fig. 3 ci mostra quello che succede alla luce che esce dalla lente. I raggi rossi convergono verso un fuoco diverso da quello della luce verde e della luce blu (e lo stesso vale anche per gli altri colori). La nostra immagine stellare si colora magicamente.

Può anche essere molto suggestivo, ma è sicuramente un difetto che deteriora l’osservazione. Siamo di fronte a un primo tipo di aberrazione che è intrinseca della lente, ossia del fenomeno della rifrazione: l’aberrazione cromatica.

Se questo difetto poteva anche essere accettato da Galileo Galilei, non può più esserlo oggi. Cosa fare, allora? Non è teoricamente difficile. Basta inserire un’altra lente dopo la prima e far convergere nello stesso punto sia la luce rossa che quella blu (i due estremi del visibile, violetto permettendo), come vediamo nella Fig. 4, in alto.

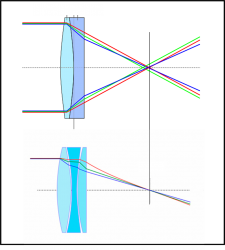
Purtroppo, far convergere gli estremi non vuol dire far convergere anche le altre lunghezze d’onda. Se volessimo aggiungere anche quella verde dovremmo aggiungere ancora una lente (in basso). Oltretutto le lenti dovrebbero anche essere di vetro diverso e di forma diversa. Oggi tutto è possibile, ma il peso aumenterebbe e anche il costo di lavorazione. Non solo, però. Dover percorrere un tragitto sempre più lungo nel vetro porta a dispersione di luce (riflessioni interne e cose più complicate) e quella finale perderebbe parte della sua energia. Insomma, le lenti, in astronomia osservativa, hanno perso molto del loro fascino antico.

Prima di abbandonarle del tutto (almeno nella nostra trattazione elementare) utilizziamone una per introdurre visivamente un’altra fonte di disturbo, ossia un’altra aberrazione di tipo geometrico: l’aberrazione di sfericità. Accidenti, ancora qualcosa che aumenta le dimensioni del disco di Airy e peggiora il potere separatore. La vediamo in modo schematico nella Fig. 5.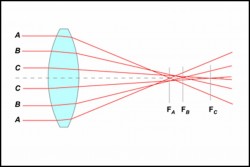 I raggi che colpiscono la lente vicino ai suoi bordi  si dirigono a un fuoco che è più vicino all’obiettivo di quanto non sia quello relativo ai raggi vicini all’asse ottico. Ogni coppia di raggi considerati nella figura ha un suo fuoco personale.

Un fuoco vagabondo

Vale la pena studiare in dettaglio questa situazione abbastanza critica. Lo facciamo, però, introducendo il secondo tipo di sistema ottico, quello che utilizza uno specchio. Tuttavia, ricordiamo che l’aberrazione di sfericità può essere annullata (o quasi) lavorando sulla singola lente. Un lavoro non certo facile. Bisogna intervenire trasformando la superficie in qualcosa di molto più complesso che in qualche modo vada a deformare l’onda piana che arriva all’obiettivo in modo che quella uscente, dopo la rifrazione, sia perfettamente sferica e abbia un solo punto di convergenza. Passando ai raggi (sempre perpendicolari alla superficie dell’onda, ricordate?) avremmo quanto rappresentato nella Fig. 6. La lente assume una forma strana e non certo facile da ottenere. Ne vale la pena? Vedremo che la risposta è positiva, ma in casi ben diversi da quelli legati a una lente usata come obiettivo.

Lo studio delle aberrazioni è oltremodo complesso e necessita di una geometria non banale. Ho cercato di renderlo elementare, almeno per quanto riguarda la più importante tra loro, quella di sfericità. Ciò che sto per mostravi richiede solo una minima attenzione, ma non si va oltre al teorema di Pitagora e alle proprietà dei triangoli simili. Roba da scuola media.

Chi vuole seguirmi non farà una gran fatica, ma comprenderà meglio cosa s’intende veramente per aberrazione. In mancanza di voglia o capacità o tempo può passare direttamente alla conclusione.

Consideriamo allora uno specchio di forma sferica, come quello rappresentato nella Fig. 7. Il raggio luminoso proviene dalla stella S ed è parallelo all’asse ottico. Sia C il centro della circonferenza che rappresenta la sezione dello specchio sferico. Il raggio luminoso, che colpisce lo specchio in P, forma un angolo α con il segmento PC, che è proprio il raggio della circonferenza r. Il raggio luminoso viene riflesso, tornando indietro e formando con il segmento PC un angolo uguale ad α (riflessione).

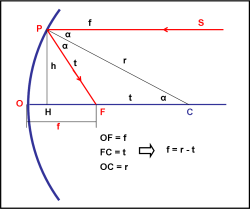
Ricordiamo che il segmento PC è perpendicolare alla tangente tracciata alla circonferenza nel punto P, ossia è proprio la perpendicolare di riferimento per la riflessione. Il raggio luminoso prosegue il suo cammino fino a incontrare l’asse ottico nel punto F. Esso rappresenta il fuoco per il raggio luminoso considerato, che dista h dal punto P di contatto (PH = h). OF è, quindi, la distanza focale corrispondente.

L’angolo PCF è uguale all’angolo SPC in quanto alterni interni di rette parallele e vale, quindi, α. Per definizione di riflessione, anche l’angolo CPF è uguale a SPC e vale ancora α. Consideriamo il triangolo PFC. Esso ha due angoli uguali (quello in P e quello in C) e quindi risulta essere un triangolo isoscele. Ma se è isoscele devono essere uguali anche i lati opposti ai due angoli uguali, ossia PF = FC. Chiamiamo t questi segmenti. Ne consegue che la distanza focale f (OF) è data anche dalla differenza tra il raggio della circonferenza-specchio (OC) e il segmento FC, uguale a t. ossia:

f = r – t

Passiamo, adesso, alla Fig. 8. Tracciamo da F la perpendicolare al raggio della circonferenza CP. I due triangoli che si ottengono sono rettangoli e uguali tra loro (due angoli e due lati uguali). E’ quindi KC = PK = r/2. Rivolgiamoci al triangolo FKC. La sua ipotenusa FC vale t e il suo cateto più lungo vale r/2.

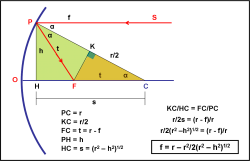
Consideriamo, ora, il triangolo rettangolo PHC. Il suo cateto più lungo HC (s) può essere ricavato applicando il teorema di Pitagora, ossia:

HC² = PC² – PH² , e quindi:

s² = r² – h²  o, ancora, s = (r² – h²)^1/2

I triangoli FKC e PHC sono simili tra loro, in quanto hanno due angoli uguali (e quindi di conseguenza anche il terzo). Se sono simili vale allora anche la proporzionalità tra i lati corrispondenti, ossia:

il cateto più lungo del primo sta al cateto più lungo del secondo come l’ipotenusa del primo sta all’ipotenusa del secondo. In termini matematici:

KC/HC = FC/PC  ossia:

r/2s = t/r = (r – f)/r

Ricordando il valore di s, si ottiene:

r/2(r² – h²)^1/2 = (r – f)/r

con semplici passaggi, si arriva a scrivere la relazione che lega la distanza focale f  al raggio della circonferenza (una costante dello specchio) e all’altezza del punto P, in cui il raggio luminoso tocca lo specchio) rispetto all’asse ottico. In altre parole, la relazione che ci permette di calcolare la distanza focale f , per ogni distanza h del raggio luminoso dall’asse ottico. Essa vale:

f = r – r²/2(r² – h²)^1/2

Nel caso in cui il raggio luminoso abbia altezza h uguale a zero (ossia coincida con l’asse ottico) si ha subito:

f = r – r²/2r = r – r/2 = r/2

il fuoco per i raggi prossimi all’asse ottico è un punto che sta proprio a metà del raggio della circonferenza-specchio. Ossia: OF = OC.

All’aumentare dell’altezza h si può facilmente calcolare che il fuoco si avvicina sempre di più al punto O, ossia la distanza focale si accorcia. Chi si vuole divertire può provare a calcolare il caso limite in cui l’angolo α è di 45°, ossia h = s. Troverà che il fuoco si sposterà fino ad H.

Questa semplice relazione ci permette di descrivere in modo oltremodo elementare gli effetti dell’aberrazione di sfericità  al crescere della distanza dei raggi luminosi dall’asse ottico.

Come si traduce, in pratica, questa variabilità della distanza focale? Lo vediamo bene nella Fig. 9.

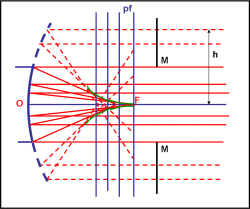
A mano a mano che spostiamo il piano focale pf  l’intersezione dei raggi che convergono verso fuochi diversi creano immagini a forma di disco che si allargano o si stringono. Il fuoco F dei raggi vicini all’asse non dà certo l’immagine migliore, dato che raggi molto lontani, come quelli tratteggiati, arrivano sul suo piano focale molto distanti dal centro.

I casi sono due: o si cerca il disco di minore estensione su un piano focale intermedio o si limita l’altezza dei raggi incidenti, utilizzando, ad esempio, un diaframma M inserito prima del contatto con la superficie sferica. Diaframma, però, vuole dire diffrazione (ricordate?). Insomma, uno specchio sferico comporta problemi non indifferenti che alterano non poco il disco di Airy teorico. L’unico vantaggio indiscusso è che la riflessione non introduce aberrazione cromatica. Inoltre, ovviamente, può permettere diametri dell’obiettivo ben maggiori di quelli delle lenti.

La figura mostra anche una curva verde, sopra e sotto l’asse ottico. Essa rappresenta una superficie che è l’inviluppo dei raggi che convergono verso i vari fuochi e definisce perfettamente l’aberrazione di sfericità. Essa prende il nome di caustica e la sua trattazione in termini analitici è oltremodo “divertente”, anche se non proprio immediata. Lo dico con cognizione di causa dato che su queste superfici di aberrazione era basata la mia tesi di laurea, tanti, tanti anni fa.

La Fig. 10 mostra un’immagine priva di aberrazione di sfericità (a sinistra) e una “raccolta”  in un fuoco intermedio in presenza dell’aberrazione (a destra). Povera figura di diffrazione!

La fantasia non basta per gli specchi

Fortunatamente la geometria viene in aiuto ai problemi che stanno riversandosi sulla nostra povera immagine stellare. Altro che punto perfetto! Assumo che chiunque legga queste pagine sappia cosa sono le coniche, ossia quelle curve che nascono dal taglio di un cono con piani più o meno inclinati. I loro nomi “propri” sono sicuramente più conosciuti: ellisse, parabola, iperbole. Tutti gli amanti del Cosmo sanno benissimo che esse rappresentano i vari tipi di orbita che un corpo planetario può descrivere attorno alla sua stella.

Ogni curva ha tutta una serie di caratteristiche esprimibili in vari modi. A noi interessano, adesso, quelle di tipo puramente geometrico. L’ellisse è quella curva chiusa tale che per ogni suo punto la distanza con due punti detti fuochi deve rimanere costante. In campo astronomico un pianeta descrive normalmente un’ellisse con il Sole posto in uno dei due fuochi. Un caso limite dell’ellisse è la parabola, una curva “aperta” simile all’ellisse, in cui si può immaginare che uno dei due fuochi vada all’infinito. Lasciamo per il momento da parte questa visione ben più generale e istruttiva e torniamo al nostro specchio sferico e ai suoi difetti di convergenza dei raggi paralleli.

Se, invece, di una sezione sferica introducessimo una sezione parabolica? Succederebbe qualcosa? Sicuramente sì. Proprio per definizione di parabola. Provare per credere. Prendete un fascio di raggi paralleli che incidono su uno specchio parabolico e costruite i raggi riflessi. Qualsiasi sia l’altezza dei raggi rispetto all’asse ottico trovereste che i raggi riflessi convergono verso un unico punto, che è proprio il fuoco dell’obiettivo parabolico, ma anche il fuoco della parabola. Vi sono tanti modi per dimostrarlo in modo analitico. Io preferisco quello legato proprio alle onde luminose che giungono fino al telescopio.

Uno dei criteri per definire una parabola è la relazione che dice che la distanza totale da una retta perpendicolare all’asse di simmetria (asse ottico) fino al fuoco è una costante. Considerando la Fig. 11, possiamo scrivere questa relazione in semplicissime forme matematiche:

QP + PF =  Q’P’ + P’F = cost.

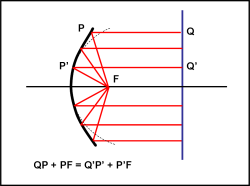
Ma la retta perpendicolare QQ’ rappresenta perfettamente un’onda luminosa piana che sta arrivando da una stella lontana. La relazione di prima cosa dice allora? Che un raggio luminoso qualsiasi, che sia perpendicolare all’onda piana, è obbligato a toccare la superficie parabolica e convergere nel punto F. Non solo, ma anche che tutti i raggi devono fare la stessa cosa. In poche parole, un fascio di raggi paralleli, dopo la riflessione su una superficie parabolica converge in un unico punto.

Le condizioni che fanno nascere l’aberrazione di sfericità sono state cancellate e quindi possiamo concludere che uno specchio parabolico non presenta questo tipo di aberrazione. Vi pare poco?

Il telescopio di Newton

Capite allora perché questo tipo di telescopio ha avuto tanto successo. Il suo nome proprio è telescopio di Newton. Esso è ottimo finché si rimane su campi abbastanza piccoli, ossia non si considerano raggi stellari troppo inclinati rispetto all’asse ottico. In altre parole: se la distanza focale è molto più grande del diametro del telescopio (ricordate il capitolo precedente). Torneremo su questo problema tra poco.

Vediamo adesso un altro tipo di problema legato al telescopio puramente parabolico. Come avete visto, il fuoco, ossia il luogo dove si forma l’immagine, è posto davanti allo specchio rispetto alla sorgente luminosa. Per guardare cosa succede nel fuoco dovremmo entrare dentro al telescopio e bloccare la luce che viene dalla stella. Bisogna fare qualcosa. La soluzione più ovvia è quella di inserire uno specchietto piano che devi i raggi che stanno dirigendosi verso il fuoco e ne crei uno esterno al telescopio. Proprio quello che si vede nella Fig. 12.

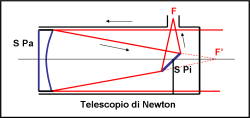
Ovviamente, se vogliamo analizzare l’immagine finale non con l’occhio, ma con altri sensori non avremo nessun bisogno di deviare i raggi e potremmo introdurre lo strumento che guarda le immagini direttamente nel fuoco reale F’. Vi sarà un piccolo ingombro, ma non quanto quello causato comunque dallo specchietto piano S Pi. Inoltre, tenete sempre a mente che introdurre uno specchietto vuole dire introdurre un ostacolo con dei margini e quindi … diffrazione!

Un altro problema del telescopio di Newton è quello dovuto al suo ingombro. Abbiamo visto che può lavorare abbastanza bene se la distanza focale è lunga rispetto al diametro. Ne segue che la lunghezza del tubo del telescopio è abbastanza lungo, poco meno della distanza focale. Se il diametro cresce troppo, il tubo diventa enorme, pesante e può subire flessioni.

Allunghiamo accorciando

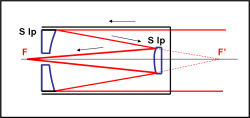
Per ridurre l’ingombro e poter, comunque, mantenere una distanza focale notevole nasce una variante importantissima del riflettore Newton, il telecopio Cassegrain. Esso sfrutta la convergenza dei raggi assiali in un unico punto data dallo specchio parabolico (senza aberrazione sferica), ma inserisce uno specchio secondario lungo l’asse dello specchio primario. Qual è lo scopo di questa “intrusione”? Semplice: rispedire indietro i raggi luminosi e farli convergere in un punto che stia oltre il primario.

Sicuramente il sistema diventa più complicato: bisogna costruire e inserire uno specchietto secondario e poi bisogna fare un buco nel primario per permettere ai raggi di convergere all’esterno, dove poter analizzare tranquillamente l’immagine finale. E’ vero, abbiamo introdotto un ostacolo alla luce che arriva dalla stella, ma abbiamo ottenuto un fuoco facilmente raggiungibile e una grande lunghezza focale con un ingombro del tubo nettamente minore.

La distanza focale finale, infatti, è quella relativa a tutto il percorso del raggio, da S Pa a S Ip, fino al fuoco F, decisamente più lunga di quella originaria da S Pa a F’. La lunghezza del telescopio è circa la metà della distanza focale, ma può anche essere minore. Un gran bel vantaggio!

Avete visto che lo specchio secondario l’ho chiamato S Ip, che sta per specchio iperbolico. In  realtà, la forma della sua superficie riflettente è un’ iperbole. La Fig. 13 mostra una classica combinazione Cassegrain.

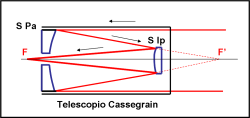
Si potrebbe usare anche uno specchio piano (il telescopio astrometrico dell’Osservatorio di Torino usa questa semplice soluzione), ma la lunghezza focale resterebbe inalterata, con un ingombro del tubo pari alla metà di essa..

I raggi si inclinano

Vi siete accorti che stiamo facendo di tutto per avere grandi lunghezze focali, ossia campi di vista molto ridotti. Soluzione perfetta per misurazioni molto precise, ma meno interessante per coprire larghe zone di cielo. Sembra quasi che abbiamo paura a ricevere immagini da stelle molto inclinate rispetto all’asse ottico, ossia tali che i loro raggi formino angoli abbastanza grandi con l’asse ottico dello strumento. In effetti, è proprio così.

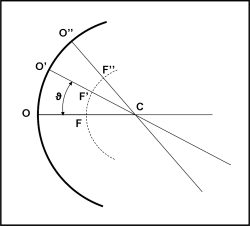
Se l’angolo comincia a crescere fa la sua comparsa la prima aberrazione fuori asse, il coma. Essa dipende dall’angolo di inclinazione ϑ che il raggio forma con l’asse ottico e, in parte, anche dall’altezza del raggio nel suo punto di contatto con la superficie rifrangente o riflettente dell’obiettivo. E’ una specie di mix tra aberrazione di sfericità (che dipende solo dall’altezza del raggio parallelo all’asse) e la deformazione dovuta all’angolo che i raggi formano con l’asse. Insomma, un bel pasticcio. Non chiedetemi la trattazione analitica che non potrebbe essere comunque banale. Vediamo, invece, in Fig. 14, uno schema molto semplificato di quello che succede per un fascio di raggi paralleli inclinati di un angolo ϑ rispetto all’asse ottico.

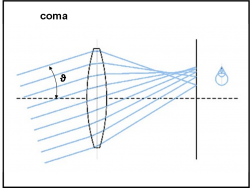
Il fuoco non è certamente unico e nasce una strana figura a “goccia”, tipica delle immagini stellari poste ai bordi di telescopi che non fanno niente per annullare quest’aberrazione. La goccia la vediamo in dettaglio nella Fig. 15

e un campo largo, affetto da coma, lo vediamo in Fig.16.

Due iperboli sono meglio di una parabola

Si può fare qualcosa per il coma? Sicuramente sì, basta studiare le superfici di due specchi che possano essere qualsiasi e vedere se esistono soluzioni che permettano di annullare sia aberrazione di sfericità che coma. Si deve abbandonare la forma parabolica del primario e fare calcoli molto accurati. La soluzione esiste e porta a due specchi (primario e secondario) ambedue iperbolici (o a curve anche più complesse).

Se volete che rappresenti questa geniale soluzione, che prende il nome di Ritchey-Chretien, avrete una piccola delusione. Ho ripreso tale e quale la Fig. 12 e l’ho riproposta in Fig. 17, cambiando solo S Pa in S Ip. Le curvature dei due specchi sono diverse da quelle di prima, ma la differenza è impossibile da notare sulla figura. L’aspetto complessivo è lo stesso. Tuttavia, adesso possiamo diminuire di molto la distanza focale (e quindi aumentare il campo di vista) a parità di diametro. Anche l’ingombro diventa minore. Non per niente è una delle soluzioni più usate in campo professionale.

Non credete comunque che con il coma ci siamo tolte tutte le aberrazioni. Ve ne sono anche altre. Una per tutte l’astigmatismo e poi la curvatura di campo e la distorsione… Insomma il percorso verso un’immagine di diffrazione perfetta non è assolutamente facile.

Non è comunque il caso di scendere ancora di più in questi dettagli. Chi usa un telescopio deve conoscerle perfettamente per non considerare, come reali variazioni topografiche di strutture planetarie, delle semplici deformazioni dovute alle aberrazioni. Quante delusioni ho dovuto dare a molti volenterosi dilettanti…

D’altra parte un ottimo Ritchey-Chretien non è certo alla portata di tutti, tranne che di qualche ricchissimo amatore giapponese. Ne ho conosciuto uno, magnate della carta di riso, che ha costruito uno strumento da 1.80 m di diametro con tanto di staff tecnico dedicato e pagato. Attorno al telescopio un parco astronomico immenso, libero a tutti. Un sogno per l’Italia, ovviamente, ma un’esperienza bellissima. Soldi spesi bene, per la cultura e per il prossimo. A volte anche i ricchi pensano ai meno fortunati. Lo sapevate che è una cosa possibile anche oggi? Un po’ come chi è ricco di esperienza e cerca di distribuirla senza alcun ritorno economico… tanto per rimanere in tema divulgazione…

La sfera è sempre la soluzione migliore

Anche il Ritchey-Chretien ha comunque dei limiti di campo visivo e bisogna andare oltre se si vuole fotografare un campo ancora più grande, necessario per lavori sistematici di ricerca, in cui le aberrazioni non siano troppo importanti anche per grandi angoli di inclinazione. Per ottenere ciò bisogna tornare all’inizio di tutto: alla superficie sferica.

Sappiamo benissimo che l’aberrazione sferica va a nozze con questa superficie (si chiama così non a caso…), ma le altre, quelle fuori asse? Vale la pena fare una breve, ma fondamentale considerazione sulla sfera e sulle sue proprietà indiscusse.

Consideriamo la Fig. 18. Trascuriamo i fasci di raggi paralleli tra loro e consideriamo solo il raggio centrale di ogni fascio, ossia quello che passa per in centro C della circonferenza. Incliniamoli pure di quanto vogliamo e vediamo se le aberrazioni fuori asse, come il coma, restano importanti. Ogni raggio che passa per il centro C della sfera può essere considerato asse ottico, dato che la sfera non ha un diametro privilegiato. Sappiamo anche molto bene come calcolare il fuoco per i raggi coincidenti con l’asse ottico. La distanza focale vale proprio r/2 (lo abbiamo dimostrato poco fa).

E’ ovvia la conclusione: se ogni raggio che passa per il centro è asse ottico, ogni raggio di questo tipo ha come fuoco un punto che sta su una circonferenza che ha ancora C come centro e come raggio proprio r/2. Questa circonferenza è il luogo delle immagini di tutti i raggi, anche quelli molto inclinati rispetto all’asse ottico, dato che (lo ripeto ancora) qualsiasi raggio che passi per C rappresenta perfettamente l’asso ottico.

Questo fatto vuol dire che la superficie sferica non ha aberrazioni fuori asse, dato che ogni raggio è un asse. Il coma è eliminato automaticamente. Rimangono due problemi, uno più semplice e uno più complesso.

Il più semplice è quello relativo al piano focale che non è un piano, ma una superficie sferica. Nessun problema. Si possono modellare i ricevitori in modo che si adattino a una forma non piana. Al limite si può anche introdurre una lente che trasformi le immagini formate su una sfera in immagini su un piano (ma non si usa molto). Il problema più importante è però quello dell’aberrazione di sfericità che resta molto importante, come abbiamo visto all’inizio dell’articolo.

Tuttavia, il gioco vale la candela. Se riuscissimo a eliminarlo potremmo avere un campo visivo molto grande e telescopi compatti con lunghezze focali corte. In realtà sappiamo come fare per correggere l’aberrazione di sfericità: interporre ai raggi paralleli incidenti una lente dalla forma strana (vedi Fig. 6) che deformi l’onda piana che arriva in un onda di forma uguale e contraria alla deformazione che causerebbe uno specchio sferico su  un onda piana.

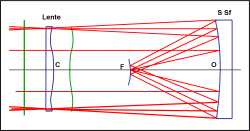
Vediamo la combinazione ottica nella Fig. 19. La lente “correttrice” C deforma l’onda piana verde e le dà una strana forma. Quest’ultima arriva sullo specchio sferico, viene nuovamente deformata e riesce a formare un’immagine puntiforme sul piano focale. Sul piano focale curvilineo in cui sta F si formano anche le immagini inclinate. Abbiamo ottenuto un telescopio Schmidt, fantastico per fotografare ampie zone di cielo e fondamentale, ad esempio, per scoprire asteroidi e comete. La sua focale può essere comparabile al diametro dell’obiettivo.

Di tutto e di più

Vi sono poi moltissime variazioni sul tema ed esistono telescopi di tipo anche molto diverso. Alcuni sono ormai obsoleti come quelli con specchi ellittici. Teniamo anche presente che oggi gli specchi sono costituiti da tanti tasselli e che sono talmente sottili che possono essere deformati in tempo reale da un computer. Arriviamo così all’ottica adattiva, di cui avevo già scritto … ma il “cerca” non mi aiuta a trovare l’articolo… Boh… se qualcuno ci riesce lo inserisca nella discussione. In ogni modo, cambiare in tempo reale la superficie riflettente serve soprattutto per l’ultimo e non meno importante difetto che viene ad aggiungersi a tutti gli altri: il seeing atmosferico, ossia quel cerchietto confuso ed esteso dovuto all’atmosfera terrestre che devia continuamente i raggi provenienti dalla stella.

L’ottica adattiva fa proprio questo. Attraverso una sorgente simulata con un laser riesce ad anticipare la deformazione dell’onda piana in arrivo e a predisporre la superficie dell’obiettivo in modo da agire in modo uguale e contrario e produrre un’immagine decisamente migliore. Un’altra soluzione più “drastica” è quella di andare fuori dall’atmosfera e Hubble ne è un esempio fantastico! Deve sempre scontrarsi con la diffrazione e con le aberrazioni, ma almeno ha un’immagine priva dello “sfarfallio” dovuto all’atmosfera… e non è poco.

Direi che possiamo terminare qui questo breve e semplificato discorso sull’ottica e sulla sua applicazione ai telescopi. Forse pochi sono arrivati fino a questo punto, spaventati dalle pochissime formule che ho dovuto inserire (non più, però, del teorema di Pitagora o cose comparabili). A coloro che hanno avuto questa perseveranza vorrei ribadire che la comprensione di ciò che ci può fornire un’immagine telescopica è molto più complessa di quanto comunemente si crede. Non basta certo aggiungere marchingegni più o meno costosi, dato che quello che si guadagna da un lato si perde dall’altro. La diffrazione, prima, e le aberrazioni dopo, completate dalla turbolenza atmosferica, creano un bel problemino per chi vuole osservare  e se l’astronomo dilettante non le conosce (o spera che le aggiunte facoltative possano risolvere tutti i vari risvolti) va incontro a profonde delusioni.

L’occhio è uno straordinario sistema ottico, addirittura fornito di ottica adattiva, che ha il solo problema della limitatezza del diametro del suo obiettivo. Cercare di fornirgli un’immagine che arricchisca veramente le informazioni fisiche non è un gioco da bambini e va capito molto bene.

Conclusioni

Concludo ribadendo che il telescopio non è un cellulare che fornisce tutto e di più, schiacciando un tasto. Il telescopio vi mette in comunicazione con amici che stanno molto lontano e l’informazione che viaggia in uno spazio quasi infinito subisce pesantemente qualsiasi piccola interferenza che entra in gioco, sia essa dovuta allo stesso spazio sia essa dovuta all’occhio supplementare che aggiungete al vostro. Pensateci bene e cercate di “aprire” il vostro cellulare cosmico e capire come funziona e cosa vi può regalare. In fondo basta conoscere il teorema di Pitagora o poco di più…

Devo dire che ho faticato non poco a descrivere l’ottica in modo così elementare, toccando non solo  i risvolti più appariscenti e affascinanti, ma anche quelli veramente fondamentali, come la diffrazione e le aberrazioni. Spero che possa servire a qualcuno e che i commenti e  le domande di ulteriori chiarimenti siano numerosi. In caso contrario, tutto sarebbe perfetto: avreste capito tutto (ne sarei lusingato) o non avreste voglia di capire (e allora la cosa non mi toccherebbe minimamente, avendo ormai capito che non è giusto che interferisca con le scelte personali). Spero, comunque, che il mio non sia stato tempo sprecato.

Ah… non abbiate paura a fare domande che possano sembrare sciocche o banali. Il semplice fatto di farle vuol dire manifestare curiosità e interesse. Vi prometto che non bastonerò nessuno!

Adesso mi prendo un bel periodo di riposo, essendo prossima la tanto attesa e simpatica trasferta a Tarquinia, seguita da qualche giorno di relax e da un’altra conferenza un po’ meno “scientifica”. Al mio ritorno vedrò le reazioni e valuterò se esistono le condizioni per continuare a divulgare così freneticamente.

Viva Galileo Galilei e i suoi seguaci!