Quante stelle ci vedono?

La domanda riguardava la scoperta dei pianeti extra solari attraverso il metodo dei transiti (Kepler) ed era la seguente: “Mi chiedo da quante stelle della nostra galassia (in percentuale) questo fenomeno (il transito) possa essere rilevabile”. In altre parole, quante stelle (e quindi loro pianeti) riescono ad accorgersi che esiste la Terra attorno al Sole, osservandone il transito davanti al disco solare? Domanda bellissima e di non facile risposta, a meno di non accontentarsi di una trattazione molto terra-terra che però è alla portata di tutti e può dare un ordine di grandezza abbastanza veritiero.

C’ho riflettuto un po’ sopra e poi ho pensato di sfruttare a pieno l’articolo che è da poco stato pubblicato sul problema generale delle occultazioni. Articolo forse noioso per molti, ma che dona la possibilità, ai pochi che hanno tempo e voglia, di divertirsi un sacco senza aver bisogno di programmi preconfezionati.

Consideriamo, allora, la prima figura di quell’articolo e semplifichiamola nell’attuale Fig. 1, ragionandoci sopra tutti assieme. Al centro c’è, ovviamente, il Sole.  Ho posto la Terra sia a destra che a sinistra, in quanto sappiamo benissimo che lei gira attorno al Sole nel periodo di un anno. Ovviamente il piano dell’orbita è rappresentato dalla retta TT. Non siamo interessati alle eclissi anulari e parziali di Sole da parte della Terra viste da altre stelle. Ossia, ai cosiddetti transiti che osserva un telescopio come Kepler. In realtà non ci interessa molto che questi transiti siano centrali o proprio al limite: l’importante è che si veda una caduta di luce del Sole a causa della Terra.

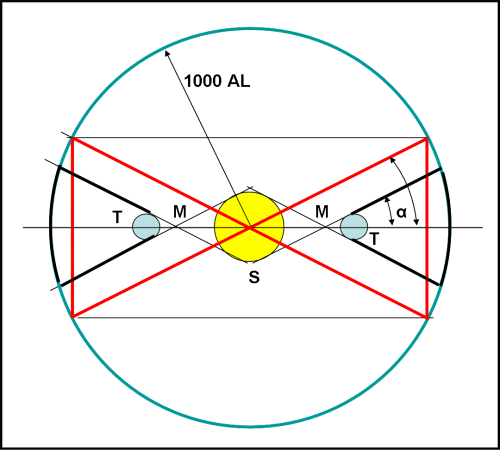
Le stelle che riescono a vederla dove si devono trovare? Ricordando la figura dell’articolo sulle occultazioni sappiamo rispondere subito. Devono essere all’interno del triangolo di penombra che si costruisce tracciando le tangenti dai bordi del Sole alla Terra dopo averle fatte incrociare. Questo triangolo ha un ampiezza pari all’angolo α, che abbiamo imparato a calcolare utilizzando il raggio del Sole, della Terra e la loro distanza, e una lunghezza che possiamo definire a piacere (basta andare sempre più lontani dal Sole). L’angolo α vale 0.0047 radianti, o, se preferite 0.27°. In altre parole, per poter vedere un transito di Terra davanti al Sole, la stella deve trovarsi all’interno dei triangoli con vertice in M e ampiezza pari a 0.27°.

A questo punto facciamo una prima approssimazione, del tutto trascurabile. Invece di considerare i due triangoli di vertice M, consideriamo i due triangoli di pari ampiezza con vertice nel Sole, definiti dalle linee rosse. Vi sembra un’ipotesi esagerata? Direi proprio di no, dato che la differenza con i triangoli di prima è pari al raggio del Sole visto dalle stelle, ossia praticamente zero.

Adesso, spingiamoci nello spazio profondo e consideriamo un cerchio con centro nel Sole che abbia un raggio pari a 1000 Anni Luce. Direi che basta e avanza per scovare alieni che ci stanno osservando. Da stelle più lontane ben pochi si accorgerebbero del Sole e noi abbiamo bisogno che non solo lo vedano ma che si accorgano dei transiti della Terra sul suo disco. Sì, 1000 anni luce possono bastare, anche se potremmo facilmente aumentare o diminuire questo cerchio.

Ormai siamo in vena di semplificazioni e continuiamo. I due triangoli rossi definiti prima sono all’interno del cerchio azzurro, anche se non hanno bordi curvilinei. In realtà, dovremmo aggiungere la parte compresa tra i bordi esterni dei triangoli e il cerchio azzurro. Vogliamo trascurarla? Io direi di sì, dato che l’angolo che la sottende è solo il doppio di 0.27° e per angoli così piccoli una corda di circonferenza può essere considerata uguale all’arco di circonferenza corrispondente. No, non facciamo un errore importante.

A questo punto devo spiegare tutto questo giro di parole e di semplificazioni (non molto azzardate per la verità). Ho cercato di disegnare, con una figura geometrica semplice, la parte del cerchio che rappresenta lo spazio attorno al Sole, in cui esistono le sole stelle che vedono il transito di Terra davanti a lui. Posso tranquillamente dire che la parte che c’interessa è quella formata dai due triangoli rossi.

Potrei concludere quasi subito, facendo qualche calcolo di matematica elementare. Preferisco, però, arrivare al risultato in modo più descrittivo e anche più comprensibile graficamente. I più preparati abbiano pazienza.

Quanto abbiamo visto finora è ciò che capita in un piano (quello del foglio) che è perpendicolare al piano orbitale terrestre (linea TT). Tuttavia, sappiamo benissimo che la Terra gira attorno al Sole e quindi la stessa cosa devono fare anche i triangoli rossi. Diciamolo meglio. Nel giro di un anno terrestre il triangolo rosso (ad esempio quello di destra) descrive una strana figura nello spazio che ha per sezione sempre il triangolo rosso. Molto più semplice è definire lo spazio stellare attorno al Sole: una sfera di raggio uguale a 1000 Anni Luce.

Come fare per calcolare quante stelle ci possono essere in questo spazio enorme in grado di vedere il transito della Terra? Immaginiamo che le stelle siano distribuite in modo omogeneo nello spazio (altra ipotesi che potremmo però sempre correggere facilmente). In queste condizioni, per sapere la percentuale di stelle che riescono a vedere il transito terrestre basta fare una divisione. In particolare, dividere il volume della strana figura rossa per il volume della sfera delle stelle intorno al Sole. Se la distribuzione è omogenea il rapporto tra il numero di stelle che ci vedono e le stelle totali è proprio dato dal rapporto dei due volumi.

Non ci resta, allora, che calcolare il volume del solido descritto dal nostro triangolo che ruota attorno al Sole. Adesso capite perché ho cercato di semplificarlo al massimo? Non avevo nessuna intenzione di fare integrali e cose del genere. Ho promesso di restare a livello di scuola media inferiore e mantengo la promessa.

Ho cercato di rappresentare nelle tre dimensioni la figura rossa rotante (Fig. 2).

Se ci pensate un attimo, non è difficile comprendere che il suo volume è quello del cilindro che ha per base il cerchio di raggio uguale a quello della sfera (ossia 1000 AL) e per altezza il segmento corrispondente all’angolo al Sole (pari a due volte  α = 0.27°), meno due volte quello del cono che ha per base la stessa base e per altezza il segmento che corrisponde proprio ad α. Il segmento che corrisponde all’angolo α (misurato ai bordi della sfera come detto precedentemente) vale 4.7 UA. Se non ci credete basta che ricordiate che questo segmento vale proprio 0.0047 x 1000 (triangolo rettangolo di cui si conosce un cateto e un angolo).

Dobbiamo, perciò, calcolare dei volumi veramente elementari. Per chi non se li ricordasse essi sono dati dalle semplici formule:

volume cilindro: π r² h

volume cono: π r² h/3

volume sfera: 4/3 π r³

Nel nostro caso specifico il volume del triangolo rosso rotante (V_V) vale:.

V_V = π 1000² x 2 x 4.7 – 2 (π 1000²  x 4.7 )/3 = 4/3 π 1000²  x 4.7

Quello della sfera (V_T) vale:

V_T = 4/3 π 1000³

Facendo il rapporto troviamo:

V_V/V_T = 4.7 /1000 = 0.0047

Cosa ci dice questo risultato ottenuto con un numero enorme di passaggi ma del tutto elementari? Che circa 5 stelle ogni mille vedono il transito della Terra davanti al Sole.

Il numero che abbiamo trovato vi indica subito che il risultato si poteva ottenere molto più velocemente. Comunque, l’importante è stato capire tutto il procedimento e sapere che con formule da scuola media abbiamo stabilito, in modo piuttosto veritiero, la percentuale di stelle che possono vedere la Terra transitare davanti al Sole, circa il cinque per mille.

Scusate se per alcuni sono stato troppo didattico, ma il risultato è comunque un risultato astrofisico, da non trascurare per niente. E ci ha anche insegnato parecchie cose.

Grazie ad AlexanderG e alla vostra volontà di mantenere sempre acceso il telefono che ci collega con l’Universo. Ricordiamoci di non spegnerlo mai e di non cercare inutili videogiochi che lo simulino. Meglio poco e nostro che tanto e anonimo.

Se qualcuno ha problemi, sono pronto a scendere ancora di più nei dettagli: nessuna paura, nessuno nasce “imparato”. Adesso, se mi passa la febbre (accidenti!), torno all’ottica.