Incontri ravvicinati con i NEO: analisi statistica (parte 2)

Analizzando gli incontri ravvicinati di asteroidi con il nostro pianeta, si nota un gran numero di “coppie” formate da oggetti passati a distanze molto simili nel giro di poche ore uno dall’altro. Di seguito, per esemplificare, ecco le coppie notate negli ultimi due mesi:

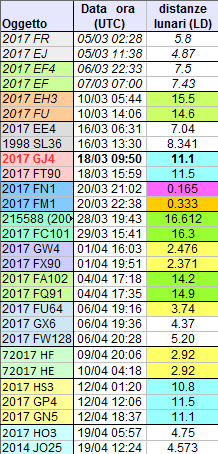
Alcuni abbinamenti sono impressionanti, in particolare la coppia 2017 FN1/FM1 (entrambi passati molto vicini alla Terra a sole 1,5 ore uno dall’altro); ci sono anche due triplette notevoli. In passato ci sono stati altri esempi ancora più clamorosi; il più noto è senza dubbio costituito dalla coppia formata da 2012 DA14 e dal bolide KEF-2013 di Chelyabinsk che, il 15 Febbraio 2013, nell’arco di 15 ore passarono a distanza estremamente ridotta (nel secondo oggetto inferiore al raggio terrestre!). Anche in quel caso, come in quelli qui riportati, le orbite degli oggetti coinvolti sono diverse (come dimostrato dalle differenti velocità) e quindi non sembra esserci una reale parentela tra essi. Eppure, si fa davvero fatica a credere che simili sequenze siano dovute al caso; prima di poterlo affermare con certezza, però, è necessaria una analisi statistica di qualche genere.

Il campione

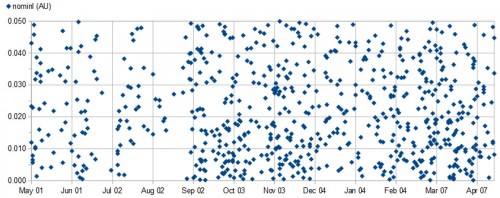
Nella precedente analisi statistica erano state analizzate le proprietà generali di un campione di quasi 500 oggetti passati entro una distanza geocentrica di 0,05 au nell’arco di 11 mesi; stavolta, sempre partendo dai dati riportati sul sito CNEOS gestito dal JPL, analizzeremo un campione un po’ più ampio ma comunque ampiamente sovrapposto al precedente. Inizialmente (prima di effettuare filtraggi) si trattava di 690 oggetti passati al distanza inferiore a 0,050 au nel periodo che va dal 1 Maggio 2016 al 20 Aprile 2017 (355 giorni); sono stati volutamente esclusi gli oggetti più recenti (a meno di 10 giorni dalla data di estrazione) per disporre di un campione di dati abbastanza consolidati, con valori più precisi (un oggetto è stato comunque escluso perchè scoperto da meno di 24 ore).

In apertura è riportato il diagramma dei valori di distanza minima nominale (sempre in unità astronomiche) in funzione della data di massimo avvicinamento;  si nota una distribuzione abbastanza uniforme in termini di distanza, mentre per quanto riguarda i tempi, i dati sembrano più diradati nel primo periodo e ci sono due veri e propri “buchi” con pochissimi eventi, uno nella seconda metà di Giugno e l’altro nel mese di Agosto. Questa disomogeneità temporale è probabilmente dovuta a due cause. Da un lato, ci sono notoriamente oscillazioni stagionali nel numero di scoperte di nuovi NEO, legate al minor numero di ore utili di buio nella stagione estiva per gli osservatori nell’emisfero boreale (che sono la maggioranza); questo è chiaramente dimostrato dal seguente grafico sulle scoperte mensili negli ultimi 7 anni (basato sempre sui dati forniti dal sito JPL nella sezione relativa alle statistiche sulle nuove scoperte):

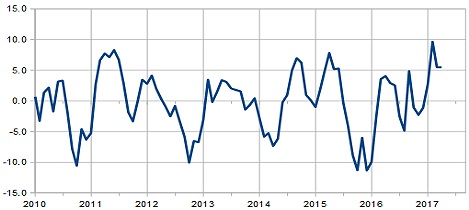
sulle ordinate c’è la differenza tra il numero di PHA noti e il numero previsto da una interpolazione sul ritmo di scoperte che non tiene conto delle variazioni stagionali; si vede come nella prima metà dell’anno c’è un eccesso che viene riassorbito nel periodo seguente, quando le scoperte avvengono a un ritmo inferiore (unica eccezione è l’anno 2014, forse a causa del maltempo).

 Un altro fattore è collegabile a un oggettivo miglioramento nel ritmo di scoperte a partire dall’autunno 2016, grazie al potenziamento dei due programmi di ricerca più importanti, il Catalina Sky Survey e il Pan-STARRS.

Filtraggio

Sulla base della disuniformità su lunga scala temporale appena evidenziata, ho deciso di limitare l’indagine agli oggetti scoperti dal 1 Settembre 2016; questo fa scomparire 124 oggetti dal campione. Un altro filtraggio necessario, come suggerito dall’analisi precedente, riguarda gli oggetti per i quali il massimo avvicinamento è noto con eccessiva incertezza, sia temporale che spaziale; questo infatti è indice di una mancata “riscoperta” o comunque di una traiettoria molto incerta a causa di un numero troppo limitato di osservazioni su un intervallo di tempo troppo breve per poter effettuare una analisi spazio-temporale come quella qui riportata; è stata scelta quindi una soglia sulla incertezza massima di 0.0010 AU sulla minima distanza e di 15 minuti sul momento di massimo avvicinamento; questo esclude altri 30 eventi portando il campione a 536 incontri.

Proprietà statistiche

Da qui in poi, ci concentriamo sulle due quantità che ci interessano, ovvero le differenze nei tempi e nelle distanze di massimo avvicinamento per coppie di incontri consecutivi, che naturalmente sono 535. Sulla base dell’intervallo temporale totale, è facile calcolare la distanza temporale media tra le coppie nel campione, pari a (230 giorni / 535) ≈ 10,3 ore; la mediana risulta essere invece di 6,9 ore. In termini di distanza minima, invece, le coppie distano in media tra loro 0.0163 UA mentre la mediana è 0.0136 UA; in entrambi i casi, dunque, la distribuzione è asimmetrica e spostata verso valori piccoli. Questo non è strano dato che entrambe le quantità dovrebbero seguire una distribuzione di Poisson.

La distribuzione temporale

Dato che la distribuzione dei passaggi ravvicinati appare abbastanza uniforme nel tempo, è possibile effettuare una analisi statistica partendo dall’ipotesi che sia davvero perfettamente uniforme. In realtà, il ritmo delle scoperte (e quindi anche degli incontri noti) segue, oltre al suddetto ciclo stagionale, anche un ciclo mensile legato alle lunazioni, in quanto il nostro satellite disturba notevolmente le osservazioni di oggetti deboli e intorno alla luna piena il tasso di nuove scoperte scende quasi a zero. Tuttavia, dato che limitiamo l’analisi a coppie di oggetti separati da un intervallo che in genere non supera le 24 ore, questa modulazione a lungo termine non dovrebbe avere un effetto apprezzabile.

Ecco l’istogramma con i conteggi del numero di coppie in funzione della loro separazione temporale in ore (sulle ascisse ci si estenderebbe fino a quasi 76 ore ma con conteggi sempre molto bassi, quindi la parte a destra è stata troncata):

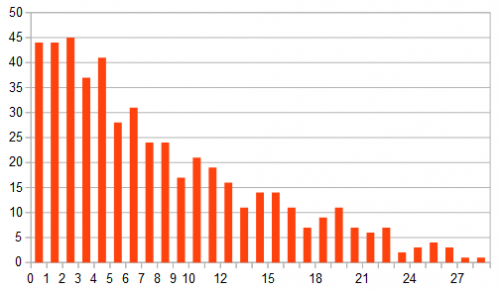
L’approccio statistico classico è quello di confrontare questa distribuzione con quella ipotetica che, come già detto, in questo caso dovrebbe essere quella di Poisson (o meglio quella di Skellam), derivata a sua volta da quella binomiale; in una fase successiva, si dovrebbe applicare un test statistico come quello del “Chi-quadro” per verificare se le inevitabili differenze sono statisticamente significative o se c’è una compatibilità con la distribuzione ipotizzata. Tuttavia, si è  preferito seguire una via alternativa, meno rigorosa e più macchinosa ma decisamente più divertente: in pratica, si è utilizzato un metodo “di Montecarlo”, generando 10 sequenze di incontri simulati casuali, tutte aventi le stesse caratteristiche della sequenza realmente osservata in termini di finestra temporale e numero di eventi; i tempi di ogni incontro sono generati sfruttando la funzione “random” presente nei principali programmi di worksheet e nei linguaggi di programmazione. In ogni tabella ho calcolato, per ciascuna coppia di incontri consecutivi, l’intervallo di tempo e alla fine ho realizzato una tabella riassuntiva con la media delle distribuzioni di queste distanze temporali, raggruppate sempre in intervalli ampi 1 ora. Il risultato è riassunto di seguito (anche qui sono state troncate le distanze temporali eccessive):

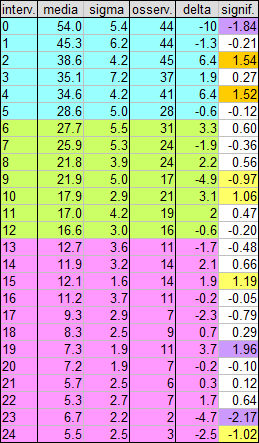
nella prima colonna è riportato il limite superiore dell’intervallo considerato, perciò la dicitura “interv.=1” si riferisce a incontri consecutivi avvenuti nell’arco di meno di 1 ora, e così via. La seconda e la terza colonna riportano appunto i valori medi e le deviazioni standard dedotti dalle 10 tabelle simulate, mentre la colonna “osserv.” si riferisce ai conteggi effettivamente osservati nel campione reale. Le ultime due colonne forniscono la differenza tra il numero di conteggi osservati e quelli simulati e la loro significatività statistica, espressa in multipli della suddetta deviazione standard. In pratica, solo in un paio di casi le deviazioni si avvicinano ad essere davvero significative (intorno ai 2-sigma, caselle a sfondo viola) ma in generale non c’è una tendenza a raggrupparsi da parte di queste deviazioni, specialmente nella zona alta della tabella che è quella che più ci interessa dal punto di vista delle “coincidenze temporali”. Di fatto, considerando tutti gli incontri separati da un intervallo inferiore a 5 ore (prime 5 righe nella tabella, con sfondo azzurro), viene fuori che il valore teorico calcolato è circa 236, molto vicino ai 239 effettivamente osservati!

Analisi spazio-temporale

Lo stesso tipo di analisi fatto sulle “distanze temporali” delle coppie di incontri consecutivi non può essere ripetuto sulle differenze in termini di minima distanza da Terra. Il motivo è che non è possibile fare una ipotesi semplicistica sulla distribuzione di questa quantità senza cadere in fallo, dal momento che sicuramente le distanze da Terra sono condizionate da un gran numero di “effetti selettivi” legati al metodo con cui i NEO vengono cercati; alcuni di questi effetti selettivi sono stati messi in evidenza nella prima parte e non è possibile “modellizzarli” in modo semplice.

Si è quindi scelto una via alternativa molto più empirica, prendendo “per buone” le due distribuzioni osservate degli intervalli spaziali e temporali e andando a verificare se queste due quantità sono tra loro  indipendenti (come è ragionevole aspettarsi) oppure se esiste davvero una tendenza a raggrupparsi su intervalli ridotti, sia spaziali che temporali. Di seguito, il grafico che mette in relazione queste due quantità (da notare la scala orizzontale logaritmica):

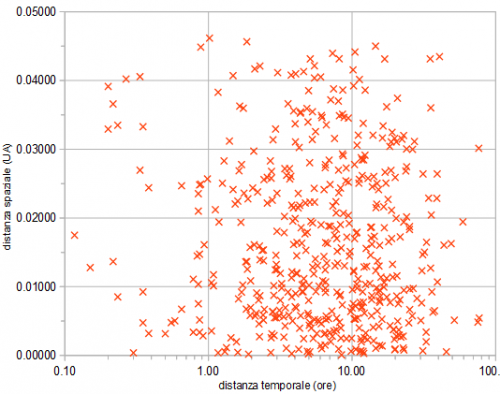
Già questo grafico suggerisce fortemente l’assenza di una sistematicità come quella ipotizzata nell’introduzione, ovvero di una tendenza di parecchi incontri temporalmente vicini ad avere anche distanze da Terra simili. Se fosse davvero così, infatti, si dovrebbe osservare un addensamento dei punti nella regione in basso a sinistra, cosa che invece non avviene!

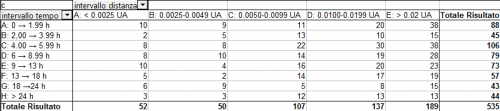
Come ulteriore test quantitativo, si è costruita una “Pivot Table” bidimensionale, in cui si riporta il numero di coppie di passaggi per diverse combinazioni di intervalli di distanza spaziale e temporale:

Si noti che stavolta gli intervalli considerati per la distanza temporale sono più ampi e diseguali, allo scopo di avere un numero consistente di incontri in ciascuna casella e non incorrere in un eccessivo “rumore statistico”. Se l’ipotesi di una indipendenza tra i valori di intervallo spaziale e temporale fosse sbagliata, anche qui dovremmo osservare dei raggruppamenti vistosi che invece non sono evidenti; per essere sicuri di questo, di seguito si è generata una tabella in cui le frequenze “simulate” si ottengono facendo semplicemente il prodotto di quelle complessive sulle distanze spaziali (ricavate dall’ultima riga in basso nella tabella precedente) e temporali (dall’ultima colonna a destra). Ecco cosa viene fuori dopo aver ri-moltiplicato tali frequenze per il numero totale di coppie:

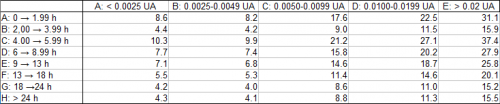
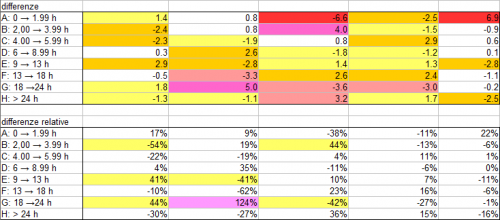
Per fare meglio il confronto, di seguito si riportano le differenze tra questa tabella e la precedente, colorando quelle più importanti; in alto c’è la tabella con le differenze assolute, in basso sono state ricalcolate con il solito metodo della significatività statistica, ovvero dividendo per la radice quadrata del numero di elementi nella tabella “teorica” che dovrebbe corrispondere, approssimativamente, a “1 sigma”:

Come si vede, l’unica deviazione in eccesso che potrebbe essere realmente significativa è quella colorata in fucsia nella seconda tabella. Tuttavia, essa è decisamente isolata, circondata da caselle in cui il saldo è generalmente negativo ; inoltre, essa non corrisponde alla tipologia di “accoppiamento” messa in evidenza all’inizio dell’articolo perchè le qui distanze di massimo avvicinamento differiscono di circa 1÷2 distanze lunari, decisamente troppo!

Conclusioni

L’analisi effettuata, anche se non particolarmente rigorosa dal punto di vista statistico, evidenzia quello che era già logico aspettarsi: le numerose coppie di passaggi ravvicinati, notate nei mesi passati e caratterizzate da tempi e distanze simili tra loro, non hanno una reale significatività e sono probabilmente frutto della tendenza, da parte del nostro cervello, a raggruppare elementi simili e cercare schemi anche dove, a volte, non ce ne sono.

Articolo originale QUI.

Articolo precedente QUI.

Ringrazio per la preziosa collaborazione corrado973.