Un viaggio alla velocità della luce e alla portata di tutti

Nella discussione dell’articolo precedente avevo inserito un filmato dell’Università del Colorado in cui si vede come ci apparirebbe il Sole (e Mercurio) se andassimo verso di lui e lo superassimo a velocità comparabile a quella della luce. I due articoli (QUI e QUI) sull’aberrazione relativistica hanno già dato le basi sufficienti per capire la strana apparenza della nostra stella e il variare dei suoi colori. Vale, però, la pena di costruire il filmato passo dopo passo (o quasi) e confrontare ciò che si vede dagli oblò dell’astronave con quello che vedrebbe un alieno posto molto lontano da lei, in un sistema di riferimento diverso e praticamente immobile (si fa per dire…). Per arrivare al termine costruiremo, prima, una specie di filmato fatto solo di fotogrammi messi in fila. Buon divertimento.

Fatemi, innanzitutto, spiegare la Fig. 1. Cerchiamo di capirla bene non solo per la spiegazione del filmato, ma anche per ripassare ciò che normalmente si vede alzando gli occhi al cielo ogni notte. E’ quindi utile a tutti, anche ai più esperti.

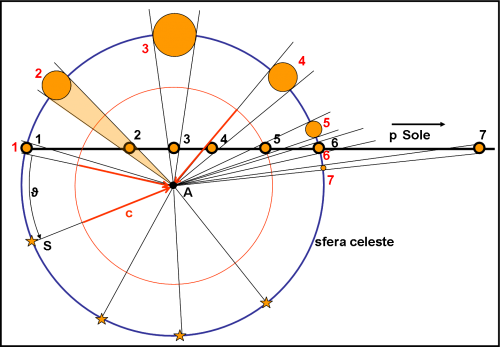
Essa non è altro che la rappresentazione simultanea di ciò che capita realmente nello spazio e di ciò che noi vediamo in cielo. In altre parole, essa descrive sia ciò che riesce a vedere un alieno posto lontano sia dalla nostra astronave che dal Sole, sia quello che, invece, vediamo noi che siamo sopra l’astronave A. Iniziamo a considerarla ferma rispetta al Sole (la pallina arancione). L’alieno vede l’astronave  in A e il Sole nella posizione 1. Immaginiamo, adesso di prendere il Sole e di spostarlo nella posizione 2. Non ho ancora parlato di velocità, ho solo preso il Sole con delle pinze speciali e l’ho spostato in un’altra posizione (gli alieni sanno fare di tutto). L’alieno, adesso, vede l’astronave sempre in A e il Sole in 2, mentre chi sta sull’astronave vede il Sole 2 proiettato sulla sua sfera celeste, di cui A è il centro, nella posizione 2.

Richiamiamo cos’è la sfera celeste. Essa è una sfera ipotetica che ha l’osservatore nel centro e  un raggio qualsiasi. Infatti, non interessa sapere quanto valga il raggio, dato che tutti gli oggetti che sono visti dall’osservatore sono proiettati sulla superficie sferica della sfera celeste. In altre parole, siamo liberi di disegnare la sfera celeste con qualsiasi raggio vogliamo. Quello che conta è l’angolo sotto cui l’osservatore vede l’oggetto celeste rispetto a una direzione fissa nel cielo. Ad esempio, l’angolo che il Sole in 1 fa con la stella S, supposta all’infinito, visto da A. Questo angolo rimane sempre lo stesso sia accorciando che aumentando il raggio della sfera celeste. La faccenda risulta ancora più evidente se consideriamo il diametro di un oggetto relativamente vicino, come il Sole, posto in 2. L’alieno vede il Sole sempre grande uguale (ha certe dimensioni angolari che non cambiano mai, data la grande distanza a cui si trova), ma l’osservatore in A lo vede più grande di quanto non l’abbia visto in 1 (dato che adesso il Sole è molto più vicino).

Le dimensioni angolari del Sole sono cambiate, ossia l’angolo colorato in arancione (relativo al Sole 2) è più grande di quello relativo al Sole 1, ma è più piccolo di quello del Sole 3. A questo punto, è del tutto analogo se proiettiamo il Sole su una sfera celeste qualsiasi, dato che il diametro apparente del Sole visto da A rimane sempre lo stesso. Non per niente, quando parliamo di dimensioni del Sole visto dalla Terra lo facciamo in termini di angolo e diciamo che vale circa trenta primi d’arco. Tutto questo discorso (forse ovvio per la maggior parte dei lettori) è stato fatto solo per poter scegliere la sfera celeste a una certa distanza da A, favorevole per il disegno. La immaginiamo passare per il Sole in 1, ma abbiamo capito benissimo che potevamo prenderla con un raggio enormemente più grande come anche con uno più piccolo. Ovviamente, per una stella S, a distanza enorme, non si parla normalmente di diametro angolare, ma solo di posizione sulla sfera celeste. Per lei, qualsiasi raggio si voglia dare alla sfera celeste, il risultato è lo stesso: un punto è e un punto rimane.

Ricapitoliamo la Fig. 1 per meglio comprendere ciò che ho voluto puntualizzare. Mettiamoci nelle condizioni di un alieno che vede il tutto da lontano. A lui non interessa la sfera celeste di A, ma la sua che è proprio il piano del foglio. Lui non ha bisogno di rappresentare la circonferenza nera (sfera celeste) né le dimensioni angolari del Sole viste dall’astronave. Lui vede solo l’astronave A e la linea orizzontale p percorsa dall’astronave A. Immaginiamo che l’astronave viaggi a una certa velocità v, piccola o grande che sia. Immaginiamo anche che l’alieno abbia puntato il suo telescopio su A e che quindi lo mantenga fisso in quella direzione. In un certo intervallo di tempo gli sembra che il Sole si muova da 1 a 2 a 3, fino a 7. In conclusione, vede il Sole muoversi lungo la linea retta p. Le dimensioni della nostra stella sono sempre uguali e ciò che vede cambiare è solo la posizione relativa del Sole rispetto all’astronave. Può dire tranquillamente che in 3 la nave ha raggiunto il punto più vicino e in 7 quello più lontano. Il moto apparente del Sole rispetto all’astronave avviene nel piano del foglio perpendicolare al suo telescopio. Non vi è componente di velocità rivolta verso di lui e quindi i fotoni inviati dal sistema Sole-astronave non subiscono rallentamenti fittizi o deformazioni. Vede, in poche parole, la scena nella sua realtà assoluta (sempre che esista qualcosa di assoluto nell’Universo). Sarebbe facilissimo fare un filmato che rappresenti questa visione aliena: basterebbe far muovere una pallina gialla lungo una retta con un puntino nero fermo al centro (l’astronave A). Nessuna variazione di colore o altre diavolerie del genere.

Consideriamo, adesso, la stessa Fig. 1, entrando dentro l’astronave A. La circonferenza rossa ha per raggio il vettore velocità della luce c, proprio quella che hanno i fotoni che partono dal Sole o dalle stelle e che giungono fino ad A. L’astronave è ferma e quindi i fotoni arrivano tutti assieme per oggetti che hanno la stessa distanza da A. All’istante iniziale giungono su A i fotoni delle stelle S e del Sole in 1, ovviamente partiti in tempi diversi (molto prima per le stelle e poco prima per il Sole). Cosa vede l’osservatore in A in quell’istante? Vede tutto proiettato sulla sua sfera celeste (che può avere un raggio qualsiasi). Le stelle S sono in una certa direzione e il Sole nella direzione 1 con un diametro angolare che è dato dall’angolo sotto cui l’osservatore vede il diametro vero del Sole alla distanza in cui esso si trova in quell’istante (ossia alla distanza tra 1 e A).

Come vedremo tra poco, Il fatto che 1 e 1 coincidano si deve solo (lo ripeto ancora una volta) al fatto che ho scelto di rappresentare la sfera celeste proprio con un raggio uguale a questa distanza. Una questione di spazio utile per disegnare e di necessità di non tracciare troppe linee che disturbino la visione complessiva del disegno. Tutto lì.

Sarebbe bello far muovere subito l’astronave e vedere cosa succede, ma dobbiamo pazientare un attimo. Sappiamo già dagli articoli precedenti che questa situazione porterebbe a un caos terrificante: colori che cambiano, direzioni che si spostano, tempi che si dilatano e altro ancora. Dobbiamo quindi andare per gradi se vogliamo fare un filmato realistico.

Mettiamo pure in moto l’astronave, ma fermiamola ogni volta che il Sole raggiunge (rispetto all’astronave considerata sempre in A) i punti da 1 a 7. In altre parole, trascuriamo ciò che vede A durante il suo moto e apriamo gli occhi solo quando l’astronave si ferma. In quei momenti tutte le varie deformazioni spariscono. Facciamo quindi un filmato composto di 7 fotogrammi, separati temporalmente tra loro. Dato che sono presi quando l’astronave è ferma, non sono minimamente toccati dalla teoria di quel signore che conosciamo ormai molto bene, ossia il dott. Einstein. Cosa vede l’osservatore in A? In 1 vede il Sole di dimensioni angolari piuttosto piccole che dipendono solo dalla distanza a cui si trova la stella in quel momento. In 2 vede il Sole, che si trova realmente in 2, proiettato sulla sfera celeste in 2, con dimensioni angolari che sono date dall’angolo sotto cui A vede il Sole 2 (angolo arancione).

Attenzione! Le dimensioni di 2 sembrano enormi rispetto a quelle di 2, ma quest’apparenza dipende solo da dove abbiamo messo la sfera celeste. Se la ponessimo ancora più lontana, le dimensioni sembrerebbero ancora più grandi. Ma, in realtà, non è assolutamente vero! Le dimensioni che contano sono quelle angolari e l’angolo non cambia cambiando il raggio della sfera celeste. Ciò che noi vediamo nel Cielo sono proprio le dimensioni angolari che dipendono solo dalle dimensioni reali del Sole e dalla sua distanza in quel determinato istante.

Altro spostamento di A ed eccoci (fermi) in 3. Il diametro angolare del Sole è ancora cresciuto. D’altra parte è ovvio dato che siamo alla distanza minima tra astronave e stella. Anche l’alieno sarebbe perfettamente d’accordo con noi, dato che anche lui vedrebbe il Sole e A alla minima distanza. Il Sole, poi, si allontana diventando sempre più piccolo (angolarmente) fino ad apparire come un dischetto appena percettibile in 7.

Attenzione! In questo caso la sfera celeste scelta ha addirittura un raggio minore alla distanza reale astronave-Sole, ma ormai sappiamo  che conta ben poco. L’apparenza nel cielo non dipende assolutamente dal raggio scelto per la sfera di riferimento. A questo punto, possiamo preparare il filmato che mostra cosa si vede dall’astronave durante il suo viaggio verso il Sole fino al sorpasso e all’allontanamento. Un filmato che va a scatti, però, eliminando in tal modo gli effetti relativistici. Esso mostra un disco solare che da piccolo diventa grande e poi torna a diminuire. Insomma niente di speciale e di veramente strano.

So di essere addirittura pedante, ma lasciatemi mostrare questo “filmato” nella Fig. 2.

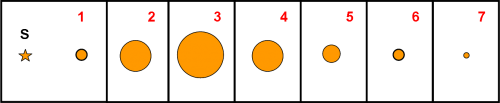
Nel fotogramma 1 ho anche inserito la stella S (non picchiatemi se l’ho messa a una distanza un po’ più piccola, ma è solo per facilità di disegno). Negli altri fotogrammi la stella è sempre nella stessa posizione, dato che il movimento dell’astronave è comunque ridicolo rispetto alla sua distanza. Notate anche che, per guardare i panorami raffigurati nei fotogrammi, l’osservatore in A ha dovuto spostarsi dal finestrone di prua a quello di poppa. Infatti 1 si vede praticamente nella direzione del moto, mentre 7 si vede in direzione quasi opposta. Ripeto ancora che i sette fotogrammi sono immagini riprese su una piccola parte della sfera celeste, dove il Sole sembra muoversi. I tempi tra i fotogrammi variano a seconda del tempo che l’astronave ha impiegato tra le varie fermate. A noi, per adesso, non interessano. Tuttavia, dato che i tempi si misurano a nave ferma, l’orologio di bordo e quello dell’alieno danno gli stessi risultati (a parte la differenza costante dovuta al tempo che la luce del sistema Sole-astronave impiega a giungere fino al simpatico osservatore extraterrestre).

Sì, lo ammetto, non è un gran bel filmato e tutti potevano immaginarselo. Non differisce molto da quello che vedremmo andando in macchina verso un enorme pallone e poi lasciandocelo alle spalle.

Le cose cambiano completamente se decidiamo di costruire un filmato continuo durante tutto il viaggio, senza mai fermare la nave e facendola andare a velocità comparabile a quella della luce. Se vogliamo, insomma, risalire in qualche modo al filmato che apre questo articolo. Più o meno sappiamo già cosa succede, dato che abbiamo letto gli articoli precedenti. Ci aspettiamo che quando il Sole è davanti all’astronave il suo colore appaia azzurro e molto luminoso anche se ancora lontano. Situazione opposta dopo averlo sorpassato: il suo colore tende al rosso sempre più scuro. Anche i tempi relativi ai vari fotogrammi subiscono deformazioni, dato che i fotoni che giungono all’astronave sono orologi teoricamente perfetti e se aumentano o diminuiscono la lunghezza d’onda sono costretti a rallentare o a correre.

Tuttavia, per ricostruire i colori e i tempi, dovremmo considerare l’ellisse che abbiamo costruita utilizzando il fattore di Lorentz. Si può sicuramente fare, ma  complicheremmo di molto le cose fino a fare confusione. Limitiamoci, perciò, a vedere come le immagini prese dalla nave in movimento deformino la posizione e la grandezza del Sole. Alla fine, potremo tranquillamente anche aggiungere i relativi colori. La parte più importante del filmato sarà, comunque, compresa appieno. Già così la trattazione non è banalissima. Andate quindi con calma e seguite passo passo le varie costruzioni.

Non spaventatevi della Fig. 3. Vado a spiegarla senza fretta e in modo particolareggiato. Seguitemi con la dovuta pazienza e attenzione.

In  fondo, eseguiamo soltanto ciò che è stato fatto nella Fig. 2 dell’articolo precedente. Sommiamo il vettore velocità della luce c a quello – v, uguale e contrario alla velocità v dell’astronave. Il procedimento lo ripeterò nella Fig. 4 e poi lascerò a voi l’applicazione a tutte le situazioni.

Ricordo solo, ancora una volta, che la somma dei vettori la eseguiamo SOLO per trovare la direzione apparente da cui proviene il fotone e NON per determinare il valore del vettore risultante, che deve sempre essere uguale a c (la velocità della luce è la stessa in tutti i sistemi di riferimento, siano fermi o in movimento). In altre parole, ci serve solo per determinare la direzione apparente del Sole mentre l’astronave sta viaggiando. Tuttavia, dato che il Sole ha dimensioni reali non trascurabili, se viste dall’astronave, i fotoni che arrivano dal bordo più lontano vengono deviati in modo diverso da quelli che provengono dal bordo più vicino. Ne consegue che anche le dimensioni apparenti (angolari) del Sole vengono cambiate durante il viaggio dell’astronave e in modo sempre diverso a seconda della direzione del Sole. Le stelle S, invece, vengono spostate in S una volta per tutte, dato che la loro direzione non varia durante tutto il viaggio (rimangono sempre molto lontane anche se ci si muove in direzione del Sole a velocità vicina a quella della luce). Lo sfondo della sfera celeste su cui si muove il Sole apparente non cambia durante il viaggio, ma solo nel breve periodo di tempo necessario per raggiungere la velocità di crociera v (noi lo immaginiamo quasi istantaneo). In quel brevissimo tempo le stelle si spostano da S a S. Poi stanno ferme.

La Fig. 4 ci mostra come ho calcolato il Sole 3 a partire da quello 3. Esso è rappresentato dal disco verde. Ho eseguito la somma dei vettori relativi ai fotoni che partono dai bordi di 3 e la velocità – v (velocità apparente del Sole). Poi ho traslato la direzione del vettore risultante fino a farla passare per A. Il punto in cui essa tocca la sfera celeste è il bordo del Sole. Ne derivano, quindi, sia la direzione apparente che le dimensioni del Sole come appaiono all’astronave. Lo stesso procedimento è stato seguito per trovare la posizione aberrata S della stella S. Come si nota facilmente, il Sole sembra trovarsi decisamente più vicino alla traiettoria dell’astronave, così come la stella. Anche le dimensioni del Sole appaiono più piccole di quelle che si avevano da fermi nella posizione 3.

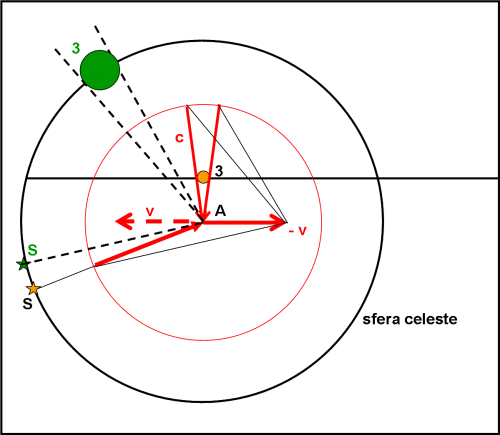
Non è difficile completare la Fig. 3. Come si vede bene, appena partiti, accelerando verso la velocità finale, il Sole si restringe e si avvicina alla traiettoria. Lo stesso fa la stella. L’apparenza è, quindi, quella di allontanamento del Sole, dato che diventa più piccolo e diminuisce la distanza tra la stella e lui. Tuttavia, in breve, il Sole inizia a ingrandirsi, anche se è sempre più avanti della posizione che avevamo trovato nella Fig. 1. A mano a mano che il Sole si avvicina, le sue dimensioni restano pressoché costanti, come anche dopo che lo abbiamo effettivamente sorpassato e guardiamo dal finestrone laterale. Poi si allontana e diminuisce il diametro angolare, ma molto meno di quanto non farebbe se visto ad astronave ferma. Malgrado sia quasi perfettamente dietro l’astronave, l’osservatore lo vede spostato in avanti nel finestrone posteriore.

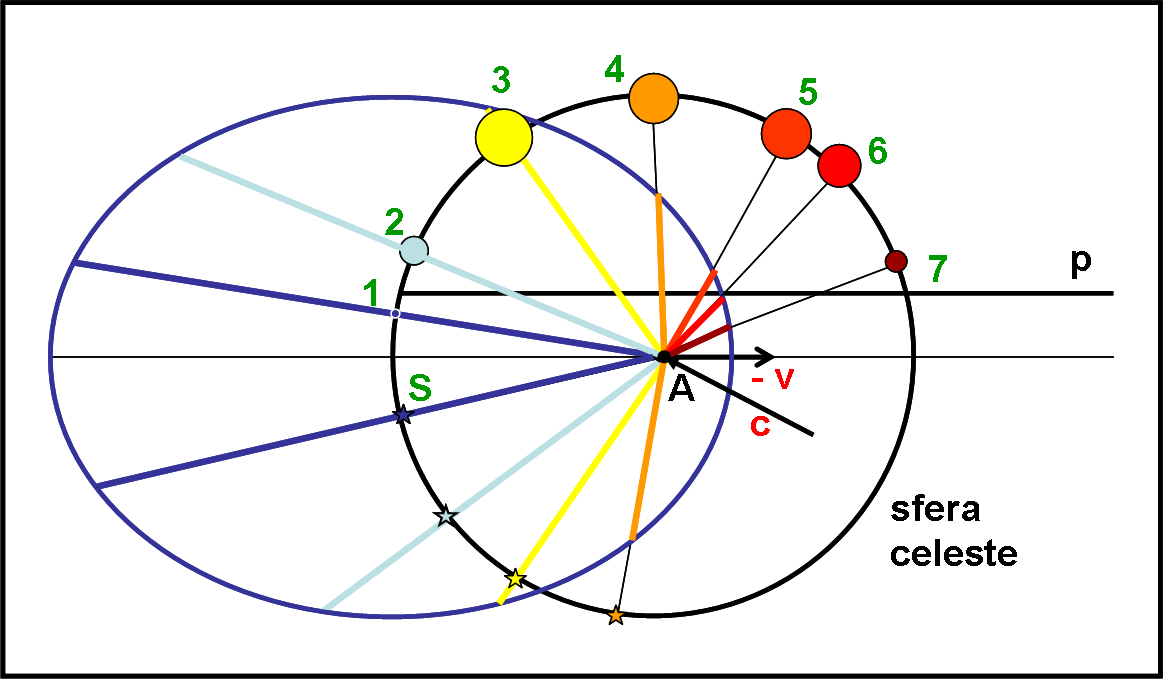
La Fig. 5 rappresenta ciò che vede l’osservatore spostandosi da un finestrone all’altro mentre l’astronave viaggia alla velocità v. Confrontatelo con la Fig. 2 che è quella del filmato preparato con singoli fotogrammi. In posizioni, che per l’alieno sono esattamente le stesse (da 1 a 7), l’osservatore in moto vede il Sole ben diversamente da quando faceva le continue interruzioni. Avremmo anche potuto fare qualcosa di più. Il Sole, in effetti, non rimane esattamente a forma di cerchio, dato che il centro si sposta verso uno dei due bordi (dopo aver applicato l’aberrazione). La sua forma sarebbe un po’ a uovo, come si può notare nel filmato vero. Tuttavia, sono sottigliezze.

Inoltre, come già detto prima, per essere veramente precisi, avremmo dovuto trasformare la circonferenza di riferimento in ellisse e, quindi, determinare quanto sarebbe diventato azzurro o rosso scuro il Sole a seconda della sua posizione. Avremmo anche capito quanto tempo ci mettono i fotoni della stella ad arrivare fino all’astronave (a volte “rallentando”, a volte “accelerando”). Anche l’aberrazione sarebbe apparsa un po’ diversa. Tuttavia, non è difficile immaginare che all’inizio, quando il Sole si avvicina, il colore varia dall’azzurro al giallo e, dopo, allontanandosi posteriormente, dal giallo all’arancione e al rosso sempre più cupo.

Non pretendiamo troppo. In fondo siamo riusciti abbastanza bene a costruire a tavolino il filmato di partenza, oltre che richiamare alcuni concetti che si pensa sempre di aver compreso bene e poi magari ci si accorge che non è del tutto vero.

Comunque, buon viaggio a tutti e ricordatevi di mettere gli occhiali scuri!