Applichiamo la diffrazione al telescopio

Avevamo concluso, con l’aiuto della perspicacia del pescatore, che un’apertura attraverso cui passa un fascio di onde piane e parallele crea un fronte d’onda che non è più piano. O -almeno- non completamente. Avevamo anche visto che il vero colpevole non è l’apertura in sé, ma i suoi bordi, ossia i punti dove si forma una discontinuità. Il pescatore aveva capito tutto ipotizzando che ogni punto dell’onda è, a sua volta, sorgente di una fascio d’onda circolare che si mescola con quelli dei punti vicini e fa apparire l’onda complessiva come piana. Tuttavia, quando l’onda attraversa un’apertura, una parte continua il suo percorso tranquillamente, mentre le onde che si originano nei punti che toccano i bordi introducono un disturbo che non riesce a essere amalgamato nell’onda piana. Dopo il passaggio attraverso la fenditura, l’onda piana si sovrappone a quelle circolari generati nei punti che la delimitano. Questo mix crea il fenomeno della diffrazione.

Per metterlo meglio in mostra si usa normalmente un’apertura estremamente piccola, dell’ordine della lunghezza d’onda, in modo che ciò che esce fuori da essa è solo l’onda circolare generatasi nei bordi, mentre quella piana praticamente non riesce a passare.

I casi di apertura larga e stretta li rivediamo nella Fig. 1: a sinistra la fenditura larga, a destra quella stretta. Nel secondo caso è come se avessimo messo in evidenza SOLO ciò che capita nei bordi della fenditura, mentre nel primo caso questo effetto si sovrappone velocemente all’onda piana che continua il suo cammino all’interno della fenditura.

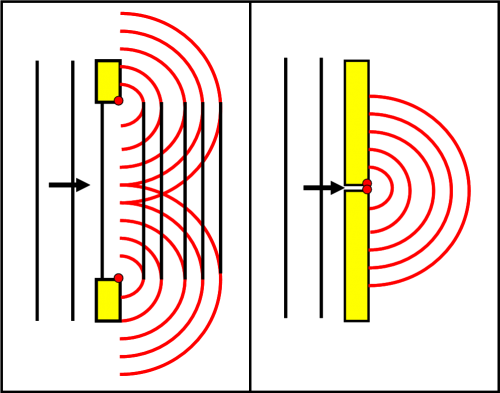
Un altro sistema per studiare le onde generatesi ai bordi di una fenditura è quello mostrato nella Fig. 2. Avevo pensato di trascurarlo, ma penso che possa servire a comprendere ancora meglio l’intero fenomeno. Consideriamo un “molo” con due aperture strette, separate tra loro (parte sinistra). Ognuna di esse produce praticamente solo l’onda circolare tipica dei bordi di una fenditura. Possiamo con relativa facilità studiare le loro sovrapposizioni e interferenze. La somiglianza di questa configurazione con quella di un’unica fenditura estesa (a destra) è più che evidente. L’unica cosa che le fa differire è il “treno” d’onda piana che prosegue oltre la fenditura (disegnato in nero), ma che non modifica più di tanto la figura di diffrazione dato che mantiene una luminosità costante lungo tutto l’asse verticale.

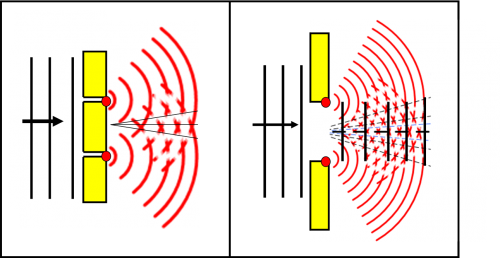
E’ quasi inutile dire che allargando e stringendo le due fenditure e/o modificando la loro distanza si ottengono figure sempre diverse che permettono uno studio accurato del fenomeno della diffrazione e di quello conseguente dell’interferenza fra onde, con una serie ininterrotta di applicazioni di estremo interesse scientifico. Ma a noi importa (per adesso) solo come questo fenomeno deformi l’immagine finale data da un telescopio (e anche dall’occhio che ha i suoi bordi come qualsiasi altro obiettivo artificiale).

La Fig. 3 introduce (finalmente !) il telescopio. Come detto, per semplicità di descrizione, considero il telescopio a specchio (ossia il riflettore)  più comune e semplice: il telescopio di Newton che è formato da un obiettivo la cui superficie riflettente è di forma parabolica in modo da trasformare le onde piane e parallele che giungono da una stella in un insieme di onde circolari che hanno il loro centro in un punto detto fuoco. Ricordate che la parabola, intesa come curva, ammette la presenza di un fuoco che ha certe caratteristiche geometriche (La Fisica Addormentata nel Bosco descrive perfettamente queste curve). Attenzione, però, a non confondere quanto detto finora: le onde circolari, che si originano ai bordi di un’apertura (o di un obiettivo) e che caratterizzano la diffrazione, hanno il loro centro proprio nel punto al bordo della fenditura. In questo caso, invece, l’onda circolare è “opposta”, ossia ha il suo centro in un punto (fuoco) lontano dall’obiettivo. Questa è un’onda che concentra la luce raccolta dall’obiettivo in un solo punto (o quanto di più simile a un punto possa essere).

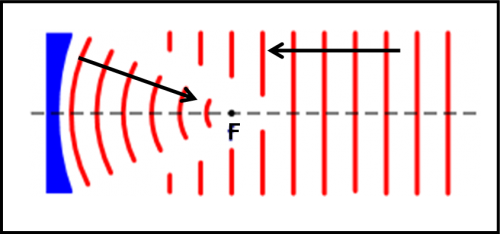
Per essere ancora più chiaro scompongo, nelle due parti della Fig. 4, ciò che fa il telescopio (tralasciando la diffrazione). Nella parte alta vediamo le onde piane, disegnate in nero, che provengono dalla stella puntiforme e lontanissima. Sono anche disegnati i raggi luminosi (già introdotti nell’ottica geometria), sempre perpendicolari all’onda piana e anch’essi disegnati in nero. Nella parte bassa l’onda piana colpisce lo specchio e viene riflessa e trasformata in onda circolare rossa (vedremo in un prossimo articolo come avviene esattamente questa riflessione). Anche in questo caso ho disegnato i raggi rossi perpendicolari alle onde circolari (in realtà non sono proprio circolari, ma possiamo tranquillamente considerarle tali…). I raggi convergono in un punto dove si forma l’immagine della stella e la cui luminosità dipende da quanti raggi sono riuscito a fare convergere, ossia da quanto è grande l’obiettivo. Dopo la diffrazione, anche la quantità di luce che si può raccogliere dipende dal diametro D dell’obiettivo del telescopio. Niente da fare: grande è bello!

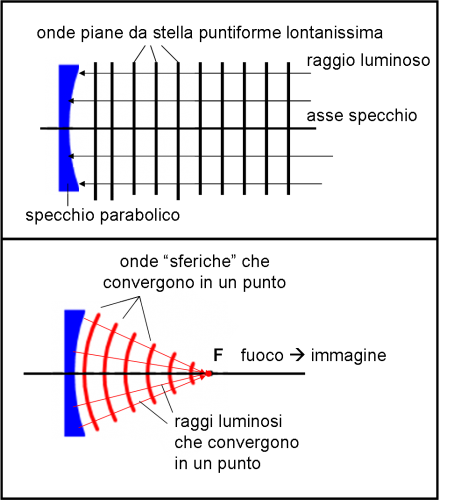
Questo schema funziona perfettamente se non introduciamo la diffrazione. Penso che ormai abbiate capito questo concetto. Senza tener conto del fenomeno della diffrazione potremmo teoricamente ottenere un’immagine puntiforme di una stella puntiforme. In pratica, non è mai vero, in quanto uno specchio introduce comunque delle imperfezioni nell’immagine, sia per la sua lavorazione sia per questioni puramente geometriche. Inoltre l’atmosfera fa “ballare” l’onda piana della stella che l’attraversa (o -se preferite- i raggi luminosi che le rappresentano). I telescopi spaziali superano quest’ultimo inconveniente e quasi del tutto quelli tecnici, ma… non possono fare niente, comunque, con la diffrazione: anche loro hanno dei bordi!

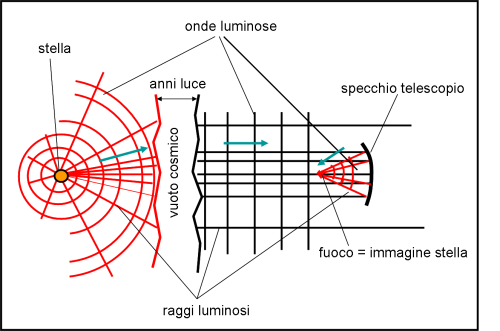
Riassumiamo l’intero tragitto della luce, sia come onde, sia come raggi luminosi, dalla stella fino al fuoco del telescopio. Lo facciamo con la Fig. 5. L’intervallo in anni luce in cui ho interrotto il percorso della luce è quello in cui le onde sferiche originali si possono, alla fine, considerare come onde piane a causa della distanza enorme e del piccolo angolo che ci raggiunge (ricordate?).

A questo punto, non ci resta che introdurre la diffrazione, l’effetto che si origina ai bordi dell’obiettivo e di cui ormai sappiamo tutto (o quasi).

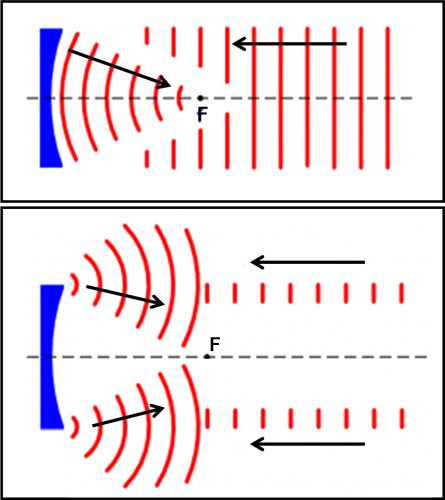
Dividiamo i due effetti che giocano sulla formazione dell’immagine nella Fig. 6. In alto riportiamo quanto abbiamo appena visto: l’onda piana si riflette sullo specchio e torna indietro come onda circolare fino a formare un’immagine teoricamente perfetta. In basso, consideriamo solo le parti di onda piana che toccano i bordi dell’obiettivo. Esse seguono le leggi della diffrazione e i due punti estremi originano due onde sferiche che si allargano andando verso il fuoco. Come già visto esse interagiscono tra loro e formano la figura di diffrazione già abbondantemente analizzata.

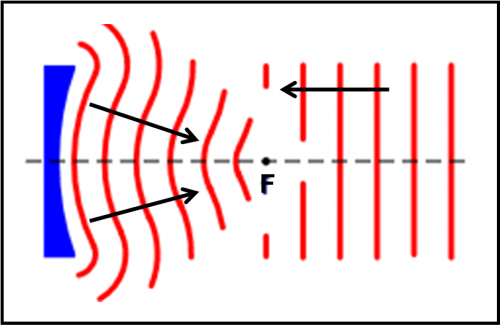
Non ci resta che mettere tutto assieme e seguire l’onda finale che giunge al fuoco. Lo facciamo in Fig. 7. Sommando le onde di diffrazione a quelle di pura riflessione si ottiene un onda di forma ben più complessa che forma nel fuoco la figura di diffrazione finale. Il disco di Airy sarà più nitido e piccolo e senza l’accompagnamenti marcato dei cerchietti concentrici quanto più il diametro del telescopio è grande (ossia quanto i due punti estremi sono distanti tra loro, come visto nell’articolo scorso). Contemporaneamente, l’immagine sarà anche più luminosa, ossia avrà raccolto più luce della stella lontana, quanto più il diametro cresce. Non è difficile notare che la quantità di luce raccolta cresce con l’area dell’obiettivo, ossia cresce con il diametro al quadrato. Su questo punto, comunque ci torneremo.

Di più sulla diffrazione e di come essa crei un’immagine NON puntiforme in qualsiasi condizione e per qualsiasi telescopio non riesco proprio a dirvi. Soprattutto non avendo voluto introdurre alcuna formula se si esclude il diametro del disco di Airy e, di conseguenza, il potere risolutivo. E, vi assicuro, non è stato facile. Se avete ancora dei dubbi, fatemeli presenti e cercherò di migliorare ancora la trattazione.

Comunque, ripeto, cercate di comprendere bene questa parte. Non la richiameremo più, ma deve rimanervi bene in testa il seguente concetto: mai e poi mai potete ottenere un’immagine puntiforme di una sorgente di luce puntiforme, qualsiasi sia il telescopio, l’obiettivo, gli oculari, la lunghezza focale, ecc., ecc. E’ inutile usare diaframmi, allungatori di focale e mille e uno marchingegni.

Dal prossimo articolo cominceremo a parlare veramente dei vari tipi di telescopi e di ciò che riescono a fare. Ci basterà utilizzare di nuovo l’ottica geometrica, ossia quella che usa solo i raggi luminosi. Tutto sarà più semplice.