BHE: un videogioco veramente spaziale!

Elimino del tutto la trattazione matematica, tenendo presente, però, che solo lei può fornire i dati da impostare e l’intera strategia del videogioco. Per adesso, mi limito soltanto a spiegare lo scopo descrivendo i passaggi fondamentali. Devo ammettere che ho semplificato, approssimato, interpretato in modo un po’ personale l’intera avventura. Posso, però, assicurarvi che segue abbastanza bene la metrica del signor Kerr e le soluzioni del signor Penrose. Ovviamente, è solo una base di partenza e spero che il “nocciolo” duro di Astronomia.com mi aiuti a migliorarlo e a trovare i punti più critici. Speriamo, poi, di risolverli insieme.

Lo schema del gioco è banale: “Bisogna entrare in un buco nero rotante e uscire in un altro universo attraverso un buco bianco”. Non solo, però, bisognerà anche stabilire in che luogo e in che tempo si  arriverà (questa sarà la seconda e più impegnativa versione di BHE, BHE.2).

Innanzitutto, dimostro perché non posso utilizzare un buco nero statico, teoricamente più facile da simulare. Il gioco terminerebbe subito e la conclusione sarebbe sempre la stessa: perderemmo comunque! La Fig. 1 ci mostra il perché. Immagino che il nostro universo sia rappresentato da una semisfera. L’altra parte del foglio contiene un altro universo, anch’esso semisferico: la meta del nostro gioco. Dato che l’universo non ha una vera forma e nemmeno una vera dimensione posso permettermelo. Ricordo infatti che le forme dell’universo normalmente ipotizzate NON sono forme geometriche, ma superfici bidimensionali che rappresentano abbastanza bene la metrica che potrebbe descrivere l’universo. Le forme sono quelle delle superfici, ma non sono la vera forma dell’universo: quella probabilmente non esiste nemmeno. Queste considerazioni mi sono state spiegate molto bene da Rosetta… Ah che bello avere per amica una nana rossa

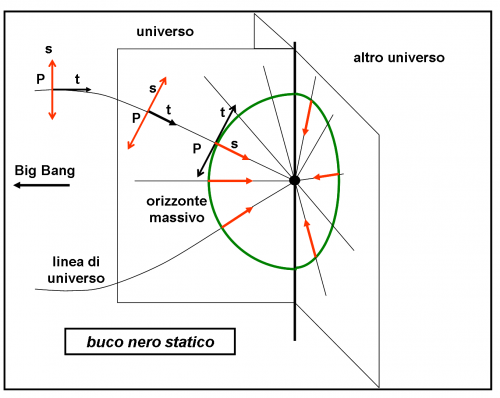
Uso, quindi, questa rappresentazione emisferica senza esitazione e seguo l’astronave P che si avvicina al buco nero. Per comodità immagino che segua la sua linea di Universo, ossia si faccia trasportare dal tempo. Questo posso farlo perché ormai chi comanda il suo movimento è la gravità del buco nero, ossia la deformazione spazio-temporale, e quindi posso immaginare che in questo sistema di riferimento l’astronave stia ferma. Ovviamente, dovrei, invece, usare il cono di luce e descrivere un movimento che tende a quello della luce. Tuttavia, sarei obbligato a deformare il cono di luce a mano a mano che mi avvicino al buco. No, troppo complicato per un gioco. Fatemi mantenere le coordinate spazio-tempo sempre perpendicolari. In fondo, non è molto importante per gli effetti che subirà l’astronave.

Davanti ad essa si para il primo vero ostacolo: l’orizzonte degli eventi. Per comodità fatemelo chiamare orizzonte massivo (non ha nessun senso fisico, ma vuole ricordare che è soltanto  legato alla massa del buco nero, dato che “lui” è statico e non ruota). L’astronave lo supera, ma fortunatamente ha le possibilità di non essere spaghettizzata (ha uno scudo anti-mareale di ultima generazione). Ciò che veramente la mette in crisi è l’inversione dello spazio-tempo. Perché capita questo ribaltamento? Beh… non posso spiegarvelo con la matematica (abbiamo detto di trascurarla), ma non è difficile capirlo. All’interno dell’orizzonte degli eventi il moto è uno e uno solo: si può andare solo verso la singolarità centrale (piccola o grande che sia). Contemporaneamente il tempo è come se si fermasse (anzi è proprio così in un certo senso). Ma, allora, è come se l’astronave seguisse una linea di universo in cui la direzione irreversibile (e fissa) è adesso lo spazio, mentre il tempo è -teoricamente- libero da “impegni”.

Ci si potrebbe muovere nel tempo? Difficile… o, almeno, per il nostro video gioco questa funzionalità non è ancora permessa (per adesso, almeno). Oltretutto, questa possibilità di moto temporale non servirebbe un granché . L’astronave sarebbe comunque trascinata verso la singolarità anche se riuscisse a muoversi “lateralmente”. Infatti, qualsiasi traiettoria possibile termina nel buco nero vero e proprio. Si potrebbe ritardare (forse), ma la conclusione sarebbe sempre una sconfitta. Un gioco in cui si è sicuri di perdere sempre non è molto avvincente. Per cui, trascuriamo il buco nero statico e consideriamo quello rotante del signor Kerr.

Ormai lo conoscete molto bene e non sto a descrivere di nuovo l’ergosfera. L’importante è che, malgrado sia una zona molto rischiosa, permette all’astronave di spostarsi e -nel caso- di uscire e riprovare a entrare al suo interno in condizioni migliori. E’ la parte più facile, ottima per i principianti, dato che spazio e tempo restano quelli che sono. Consiglio ai giocatori alle prime armi di soffermarsi su di lei e fare molti tentativi in situazioni diverse: prenderanno dimestichezza con il vero antagonista che sta aspettando “doppiamente” protetto.

La Fig. 2 mostra la situazione per chi decide di passare al livello superiore: superare l’orizzonte massivo. Vi prego, non ditemi: “Ma, allora, ricadiamo nella situazione di prima… il gioco ci vedrà sempre sconfitti”. Avreste ragione nell’affermare che vi è stato il ribaltamento spazio-tempo e che l’astronave può solo cadere verso la singolarità, ma… adesso, tra lei e il “mostro”, c’è una altra barriera da superare. Bisogna proprio giocare con questa per essere pronti a sconfiggere il nostro nemico-amico finale. Ecco che allora si capisce quanto possa essere importante la fase preparatoria (nell’ergosfera). In quella zona potremmo ancora scegliere il punto migliore per superare nel modo migliore l’orizzonte massivo. Questa volta, infatti, anche se apparentemente sembra tutto uguale al caso statico, non tutte le traiettorie sono uguali.

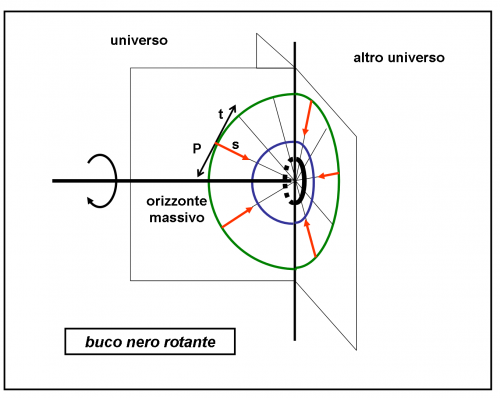
Consiglio, infatti, di prepararsi per tempo, dato che dopo la seconda barriera potrebbe non esserci più … “tempo”. Prima di proseguire, notiamo che al centro della Fig. 2 la singolarità è diventata un anello di materia o di quello che preferite. E’ un anello perché è un punto costretto ruotare in modo rapidissimo e la soluzione più ovvia è che si trasformi proprio in un anello di dimensioni… nulle. No, no, possiamo considerarlo reale, non preoccupatevi. Basta scegliere la “materia” giusta. L’astronave (preparata o non preparata a questo passaggio) supera l’orizzonte rotante (nuovamente una definizione di comodo, tanto per ricordare che è quello legato solo alla rotazione del buco nero) nella Fig.3.

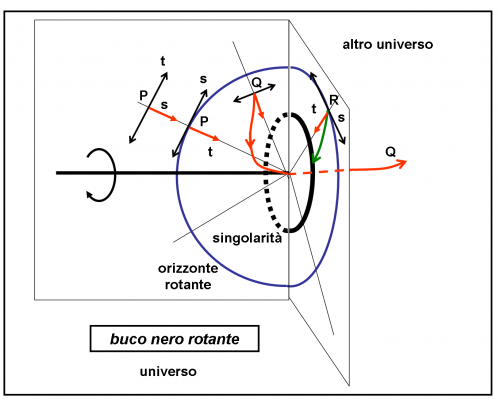
Come previsto lo spazio e tempo si invertono di nuovo (fidatevi… lo fanno “quasi” sicuramente, almeno così assicura il signor Kerr). Non vi è molto “tempo” a disposizione, dato che ormai siamo vicini al buco nero, ma adesso l’astronave è libera di muoversi nello spazio: il tempo la trascina, ma i motori possono entrare in azione. Cosa può fare esattamente? Facilissimo: cercare di non finire nel piano perpendicolare all’asse di rotazione del buco nero. Se, infatti, viaggiasse sul quel piano (come l’astronave R) qualsiasi traiettoria riuscisse a effettuare (linea verde) non avrebbe scampo e finirebbe sulla “materia” che compone l’anello. Questa soluzione è simile a quella del buco nero statico: vincerebbe “lui”.

L’ideale, per potere evitare il “contatto” con la materia del buco nero, è di arrivarci praticamente lungo l’asse di rotazione, ossia scegliere il buco nel … buco, stando bene attenti a non toccare i bordi dell’anello. Ecco perché era possibile già inserirsi nella direzione giusta prima dell’orizzonte massivo, quando si era ancora nell’ergosfera. Tuttavia, l’astronave Q ha ancora un margine di azione e può spostarsi per scegliere la giusta direzione. Questa parte estremamente delicata è stata studiata molto bene da un grande giocatore del passato: il signor Penrose. Il suo record è ancora imbattuto!

Se il giocatore si è mosso bene, e per tempo, può raggiungere il centro dell’anello. Vittoria? Praticamente sì, anche se bisognerà sfruttare una strana reazione del buco nero che si verifica soprattutto in quella particolare posizione. Accenno solo a un concetto, che dovrà essere sviluppato in dettaglio sfruttando la metrica del signor Kerr e le traiettorie del signor Penrose: lo spazio è percorribile, ma è diventato negativo. No, non spaventatevi e mantenete la rotta senza esitazione. Spazio negativo vuole dire repulsione invece di attrazione. La singolarità vi caccerà lontano da lei invece di attrarvi. E’ solo un momento, ma va sfruttato al meglio. La porta si apre e l’astronave si trova nell’altro Universo. Sarebbe lei la vincitrice della prima versione (più semplice) del videogioco.

Più interessante sarà sicuramente la seconda versione, la BHE.2. Una volta entrata nell’altro universo, l’astronave dovrà superare nuovamente le due barriere prima di entrare in un’altra ergosfera ed essere libera di viaggiare nel cosmo alieno. Potrebbe, però, uscire anche in un’altra zona (irraggiungibile con i mezzi normali) di quello già conosciuto. Perché capita questo? Lo accenno soltanto. Appena usciti dall’anello l’astronave si trova in un buco bianco, dove tutte le linee di universo vanno al contrario. Insomma, proprio come se fosse di nuovo all’istante del Big Bang.  Spazio e tempo continuerebbero a invertirsi tra loro, senza, però, il rischio di  essere ricacciati indietro verso la singolarità. Tuttavia, ad ogni passaggio di orizzonte, non si saprebbe mai in che spazio e in che tempo sia veramente l’astronave, anche perché sarebbe costretta a fare alcune manovre per scegliere le migliori traiettorie. Non parliamo poi del caos che troverebbe nell’ergosfera. Beh… questa parte del gioco è ancora in fase di studio. Per completare la BHE.2 non bastano nemmeno più i due signori di prima. Loro possono solo dirmi che si “esce” in qualche modo, ma non ancora dove e quando. Questo tocca a noi…

Allora, ci state ad aiutarmi?  Ci vuole sicuramente una persona bravissima con il computer (io no!) e forse non solo… Boh… io l’ho buttata lì. Penso che il gioco, anche solo nella versione BHE, possa farci ricchi e insegnare l’universo anche a chi non vuole conoscerlo più di tanto. Trattandosi di un videogioco avrebbe molte più speranze di riuscire a smuovere l’apatia. Non credete?

Se poi va male, pazienza… ci siamo divertiti a capire meglio i buchi neri . Imparare è sempre una vittoria!

//