Tra le varie prove sperimentali eseguite per dimostrare la costanza della velocità della luce rispetto a qualsiasi sistema di riferimento, vi è la geniale intuizione di De Sitter. Un’idea estremamente semplice e poco conosciuta ai più: le stelle fantasma.
Nel 1913 l’olandese De Sitter, una grande mente raramente ricordata, ha fornito una splendida prova osservativa. Con osservazioni astronomiche “mirate” egli ha dimostrato, come ipotizzato da Einstein, che la velocità della luce non può sommarsi ad altre velocità: è quella che è, in qualsiasi sistema di riferimento ed è il valore massimo raggiungibile. Senza bisogno di strane apparecchiature, né di lavorare con numeri infinitesimi, egli guardò direttamente all’Universo e a oggetti che si potevano vedere un po’ dappertutto, a qualsiasi distanza e con caratteristiche sempre diverse. Tra tanti esempi reali, ci sarebbero stati sicuramente quelli che servivano a lui.
Stiamo parlando dei sistemi binari di stelle. Il problemino cinematico è quello illustrato nella figura. La stellina rossa rivolve attorno alla compagna gialla con un certo periodo di rivoluzione P. Consideriamo la sua posizione in A. Essa sta muovendosi in verso opposto a quello della Terra con velocità v. In meccanica classica, la luce che viene inviata verso di noi è determinata vettorialmente dalla velocità c della luce, a cui deve essere sottratta quella dell’astro che viaggia in senso opposto.
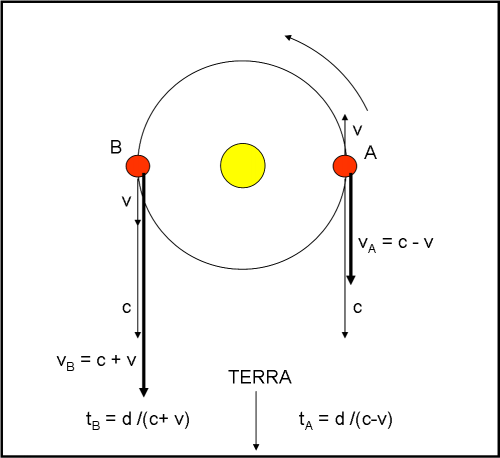
Quanto tempo impiega per arrivare sulla Terra la luce di A? Sia esso tA, dove d è la distanza della stella binaria da noi. Ricordando che la velocità è uno spazio diviso per un tempo, abbiamo:
tA = d/(c – v)
Dopo un mezzo periodo di rivoluzione, la stellina rossa si troverà in B. In quelle condizioni essa si muove verso di noi con velocità v. Velocità della luce e velocità orbitale si sommano. Quanto tempo impiega ad arrivare sulla Terra la luce di B? Sia esso tB, dato da:
tB = d/(c + v)
Si vede subito che la luce partita da A viaggia più piano della luce partita da B. Ne consegue che impiega più tempo per giungere a noi (tA > tB). E’ facile calcolare la differenza tra i tempi di percorrenza della distanza d da parte della luce di A e di quella di B. Essa è data da:
tA – tB = d(1/(c-v) -1/(c + v)) = 2dv/(c2 –v2) … (1)
Potrebbe capitare che la luce partita da A arrivi all’osservatore nello stesso istante di quella partita da B ? Abbiamo visto che quella di A viaggia più lenta e quindi potrebbe benissimo accadere. Basta che la differenza di tempo scritta in (1) sia proprio uguale alla metà del periodo di rivoluzione. Se questo fosse vero, la luce di A arriverebbe con una differenza di tempo rispetto a quella di B proprio uguale al tempo in cui la stellina rossa ha percorso metà della sua orbita. Cosa vorrebbe dire tutto ciò?
Facile! L’osservatore sulla Terra dovrebbe vedere nello stesso istante la stellina sia nella posizione A che nella B.
E’ una situazione impossibile da ottenere praticamente? Nemmeno per sogno. Basta che la quantità
2dv/(c2 –v2) sia uguale a P/2.
Tra le tantissime stelle doppie osservabili ce ne sono molte che soddisfano questa relazione. Ricordiamoci che essa dipende sia dalla velocità di rivoluzione v, sia dalla distanza d da noi, sia dal periodo P. De Sitter ne aveva indicate un certo numero, ma in nessun caso è stato possibile vedere sdoppiarsi la stellina. Essa rimaneva un vero fantasma! L’unico modo per spiegare la mancanza degli “spettri” (quelli veri, tipo castelli inglesi…) era che c + v = c -v = c, come enunciava la teoria della relatività.
Con un po’ di cinematica è possibile risolvere problemi enormi. Eh sì, la fisica è proprio una bella addormentata…
Alla prossima!
//



Straordinariamente semplice ed efficace! Bellissimo esempio, Enzo! E un grandissimo De Sitter....
Bello! Semplice, elegante ed efficace!
Era un po' che ero alla ricerca di una dimostrazione alla mia portata del fatto che C fosse costante, ed eccola finalmente qua!
Grazie Enzo!
Ciao Enzo... leggere questo articolo mi ha quasi illuso di aver finalmente realizzato un mio piccolo sogno nel cassetto, mi spiego meglio: mi riconosco molto in te e nel tuo desiderio di spiegare le meraviglie che si nascondono nella realtà quotidiana con mezzi e parole semplici, quasi per bambini... e sotto questo aspetto ho anch'io un desiderio. Io voglio poter spiegare ad un bambino di 10 anni (molto paziente) che se ci muoviamo invecchiamo di meno.. (infinitamente poco , ma di meno) però per poter proseguire ho bisogno innanzitutto di sapere se è corretto quello che ho appena scritto. Scusa l'ingenuità ma almeno la tua risposta mi darà o meno una certezza...
In ogni caso a tua disposizione...
Buon lavoro!!!
se esiste una dimostrazione dell'invarianza di c con termini esclusivamente matematici ho completato il mio racconto che mi prometto di scriverti per intero un giorno! "se ci muoviamo il tempo rallenta: basta il + il - il X e il / "
la mia dimostrazione ruota intorno all' esperimento di Michelson-Morley comunque...
le stelle fantasma dimostrano l'invarianza della velocità della luce e non ancora che il tempo rallenta...
Tuttavia, penso che la dimostrazione data da De Sitter fa solo uso dei segni che dici tu...
Sto scrivendo un articoletto che, invece, partendo dalla costanza della c, trova il fattore di Lorentz, ossia querllo che ti permette di dilatare il tempo. E tutto solo applicando il teorema di Pitagora. Insomma, matematica elementare. In ogni modo, devi prima convincere il bimbo o bimba che la c è sempre uguale. Le stelle doppie sono l'esempio più facile e terra-terra alla portata sicuramente di un bambino... Perchè dici che non basta?
Comunque aspetto il tuo racconto con grande interesse...
ho l'impressione che stiamo parlando dello stesso metodo
faccio un sunto di quello che è il racconto completo che sto scrivendo:
1) parto dall'esperimento di Michelson-Morley e lo traduco in un gruppo di persone compatte che camminano formando un quadrato. accanto a queste persone c'è un cagnolino che corre dalla coda alla testa del gruppo e torna indietro. Un secondo cagnolino invece corre percorrendo la coda del quadrato su e giu... i cagnolini corrono alla stessa velocità. è facile dimostrare che piu il plotone di persone cammina veloce e più il cagnolino che deve percorrere due volte il tragitto coda-testa rimane indietro rispetto all'altro cagnolino. (questo perchè rimane piu tempo nella condizione svantaggiosa di dover rincorrere il gruppo sottraendo la velocità del gruppo alla sua e meno tempo nel tornare indietro con la sua velocità sommata a quella del gruppo).
2) ovviamente sappiamo che se i due cagnolini fossere due particelle di luce impiegherebbero lo stesso tempo a concludere il percorso di andata e ritorno, indipendentemente dalla velocità del plotone, ma come è possibile? i casi sono due:
o il plotone si è accorciato nel senso della lunghezza (trasformazione di lorentz) o il tempo si è dilatato .
è facile che non mi sia espresso molto chiaramente ma ti assicuro che scritto con calma con tutte le relative formulette si arriva facilmente alle trasformazioni di Lorentz.
Come vedi mi manca un passaggio: il punto 2) da per scontato l'invarianza di c, dunque non voglio che il passaggio chiave sia una dimostrazione sperimentale (potrei utilizzare quella appunto dell'esperimento di Michelson-Morley del 1887 in cui si è visto che le due particelle impiegano lo stesso tempo nonostante la placca metallica quadrata si muovesse o utilizzare appunto questo tuo articolo, anch'esso esatto ma basato su osservazioni)
tutto qui, ma magari una prova matematica dell'invarianza di C non esiste per sua stessa natura, non so...
Non è invece possibile dimostrare matematicamente che c = cost. (se non a posteriori, ma non serve più per il tuo scopo). Devi accettare che è un dato sperimentale e scegliere il metodo più facile. Le stelle doppie mi sembrano più intuibili dell'interferometro...
Comunque, complimenti...
p.s. se mai ti capitasse tra le mani la dimostrazione matematica di c = cost fammelo sapere