Come ti “blocco” un satellite

Cari amici… purtroppo l’apparizione in questo sito di una serie di forum astronomici ha evidenziato una mia caratteristica finora nascosta (anche a me stesso): non riesco ad accettare domande infantili da parte di chi dice di essere appassionato dell’Universo e delle sue meraviglie. Accostarsi all’astronomia senza cercare di crearsi prima i fondamentali della matematica, della geometria e della fisica è, per me, un’assurdità bella e buona. Ancora più grave é non sentirne il bisogno. E’ colpa della scuola che è scesa mostruosamente di livello o della TV che pretende (e ci riesce) di dare tutte le risposte (sempre che le ritenga veramente “utili”)? Sia come sia, reputo impossibile rispondere a chi non sa le cose più ovvie e banali. Le risposte servirebbero a poco e, a mio parere, creerebbero ancora più confusione.

Ma questo, ormai, lo sapete molto bene. Non per niente ho deciso di non rispondere alle varie sezioni del forum se non quando i commenti e le domande non siano davvero pertinenti e giustificabili. So di essere diventato antipatico ai più… pazienza. Spero che resista un nocciolo duro che capisca le mie motivazioni e le condivida. In fondo, è solo un tentativo per cercare di indirizzare le menti verso il loro vero scopo: ragionare, riflettere, valutare, imparare…

Come dicevo, molte volte le domande hanno, invece, un senso e l’argomento merita di essere affrontato. E’ questo il caso del “blocco” della rotazione della Luna. Bisogna, però, tener presente che per rispondere a un quesito, anche non difficile, è necessario fare uso di termini e concetti a esso collegati. Sarebbe impossibile partire da zero. Se parliamo di effetti mutui tra corpi planetari bisogna avere nel proprio bagaglio nozioni come la rivoluzione attorno al Sole o attorno ai pianeti, la forza di gravità, il momento angolare e via dicendo. Senza questi, le risposte potrebbero anche spiegare approssimativamente un fenomeno, ma la sua vera essenza resterebbe slegata dal resto e sarebbe una semplice nozione in più e non un vero passo verso il quadro generale.

Ovviamente, se parlo di marea, dovrei cominciare dalla definizione di forza, di momento angolare, di legge di Newton, di forma delle orbite, di periodi, di risonanze e molto altro ancora. Ecco perché Francesca e io abbiamo scritto il libro. Proprio per cercare di dare la necessaria infarinatura di base e poterne poi discutere insieme ai lettori. Speravamo che questo tentativo venisse compreso e invece ci ha dimostrato come la lettura e la comprensione siano difficoltà enormi al giorno d’oggi.

Ovviamente non posso obbligare nessuno a comprare il volume e quindi è ovvio che le spiegazioni mirate a un singolo argomento che compariranno come singoli articoli non potranno spiegare tutto ciò che gli sta attorno. Cosa, questa, che lo renderebbe, invece, inseribile in un più ampio contesto.

Fatta questa dovuta premessa (ripetitiva, ma spero di essere compreso da un numero sempre maggiore di lettori), affronto oggi il problema della sincronizzazione del periodo di rotazione di un  satellite con quello di rivoluzione attorno al pianeta. In parole povere voglio rispondere alla domanda: “Perché la Luna ci mostra sempre la stessa faccia?” Vedremo che ciò non capita solo per il nostro $satellite$, ma per tutti i satelliti di dimensioni abbastanza considerevoli. Ho già parlato di marea in altri articoli apparsi nel sito. Ho deciso, però, di introdurla nuovamente, anche se in modo molto superficiale, per spiegare meglio l’argomento nel suo contesto generale. Per quanto possibile, ovviamente…

Consideriamo, allora, un pianeta e un suo $satellite$. Immaginiamo che ognuno dei due ruoti con un periodo diverso e che diverso sia anche il periodo di rivoluzione. Sappiamo molto bene che il moto orbitale di un corpo attorno a un altro deriva dalla legge di gravitazione universale di Newton e che le possibili traiettorie sono descritte sufficientemente bene dalle leggi di Keplero. Per quello che ci interessa non vi è bisogno di introdurre argomentazioni relativistiche (per adesso almeno).

Tutto sembrerebbe essere in perfetto equilibrio a parte le perturbazioni causate sul sistema pianeta-satellite dagli altri pianeti. Ammettiamo, però, che queste siano trascurabili. Niente dovrebbe cambiare la configurazione raggiunta. Ed ecco, invece, comparire la marea.

Cos’è la marea? Presto detto: è un effetto aggiuntivo introdotto dalla forza di gravità su di un oggetto di dimensioni abbastanza considerevoli e posto a una distanza relativamente modesta.

Un $satellite$ di forma sferica rivolve attorno a un pianeta anch’esso sferico. La sua rotazione è, per esempio, più veloce della rivoluzione. Per il momento non interessiamoci della rotazione del pianeta. Immaginiamo inoltre, per semplificare l’approccio, che con una bacchetta magica si riesca a congelare la configurazione del sistema pianeta-satellite a un certo istante. La Fig. 1a ci mostra questa situazione.

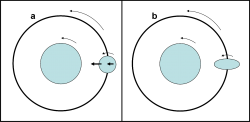
Cosa succede? Un fenomeno molto interessante e fondamentale per ogni tipo di interazione pianeta-satellite, ma anche per molti altri oggetti dell’Universo. La gravità che il pianeta esercita sul $satellite$ è più forte sul lato del $satellite$ che guarda il pianeta ed è, invece, più debole sul lato opposto. Per capire questa asserzione basti pensare che la forza di gravità diminuisce con il quadrato della distanza. Ovviamente, questo effetto è importante solo se le dimensioni del $satellite$ non sono trascurabili rispetto alla distanza pianeta-satellite, come già avevo accennato prima.

Cosa ne consegue? Che la parte del $satellite$ più vicina al pianeta tende ad allungarsi verso di lui, lungo la linea che congiunge i loro centri di massa. Il risultato è una cambiamento della forma del $satellite$ che si deforma assumendo una struttura a ellissoide (Fig. 1b). A questo punto usiamo di nuovo la bacchetta magica e rimettiamo in moto il sistema. Se il $satellite$ fosse perfettamente deformabile, indipendentemente dal suo periodo di rotazione, dovrebbe assumere istante per istante, durante la sua rivoluzione, una forma allungata diretta verso il centro del pianeta.

ATTENZIONE! questo non vuole dire che mostrerebbe sempre la stessa faccia al pianeta, ma solo che la sua forma istantanea sarebbe un ellissoide diretto verso il centro del compagno più massiccio. Una montagna o un cratere si muoverebbe molto più velocemente e sparirebbe presto alla vista del pianeta. Se, all’istante t1, una certa caratteristica superficiale A si trovasse proprio di fronte al pianeta, sulla punta dell’ellissoide, all’istante successivo t2 si sarebbe già spostata verso una zona molto meno deformata dalla marea (ossia in una parte meno curva dell’ellissoide) come indicato nella Fig. 2.

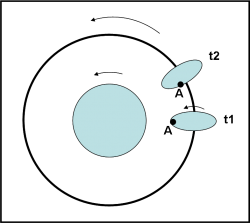
Tuttavia, i corpi planetari non si deformano a piacimento senza cercare di ribellarsi. Le forze che tengono unite tra loro le varie parti del $satellite$ (forze di stato solido) si oppongono come possono a questo “stiramento” dovuto alla marea. Alla fine sono costrette a cedere, ma ciò comporta un “ritardo” nella deformazione dominata dalla marea. In altre parole, la deformazione avviene un po’ dopo che l’oggetto ha subito la marea. Nel frattempo, però, la veloce rotazione attorno all’asse trascina con sé una forma deformata che non è più diretta verso il centro del pianeta. La situazione è, allora, quella della Fig. 3, dove la configurazione reale al tempo t2 è quella indicata dall’ellissoide rosso, dove, come già detto, il rigonfiamento viene trascinato avanti dalla rotazione del $satellite$.

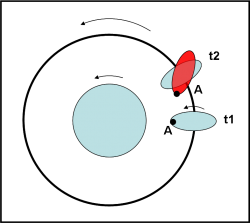
Adesso però le cose cambiano… e come! La forza di gravità del pianeta che agisce sul rigonfiamento del $satellite$ non passa più lungo la congiungente i due centri, ma è fuori asse rispetto a essa. Si crea un “momento”, ossia la forza tende a far ruotare il corpo che la subisce. E’ come quando si dà un colpo “di taglio” a un oggetto e questo si mette a ruotare. Lo potete verificare con qualsiasi cosa abbiate vicino a voi sul tavolo. Dato che il rigonfiamento è più avanti della posizione teorica, la rotazione impartita dal momento va in verso opposto a quello delle rotazione iniziale (Fig. 4).

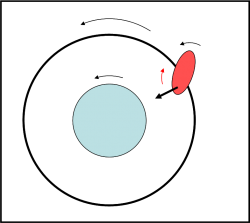
La velocità di rotazione finale diminuisce, ossia il periodo di rotazione si allunga. Questo fenomeno continua ad agire fino a che…

Potete facilmente rispondere voi! Fino a che il periodo di rotazione diventa proprio uguale al periodo di rivoluzione del $satellite$. In questo caso, infatti, la parte allungata rimane sempre la stessa, anche fisicamente, e il $satellite$ mostra sempre la stessa faccia al pianeta.

Ciò è successo per la Luna e per i satelliti maggiori di Giove, Saturno, Nettuno e Urano. Ossia, per tutti gli oggetti che siano abbastanza grandi e vicini al proprio pianeta.

Quanto detto vale per un periodo di rotazione inizialmente più rapido di quello di rivoluzione. Tuttavia, il meccanismo funziona, ovviamente, anche per il viceversa. In questo caso, il momento causa un aumento della velocità di rotazione (lascio a voi la figura esplicativa di questa configurazione. Sarà una prova per confermarvi di aver capito il meccanismo).

Per satelliti lontani, la configurazione finale ha bisogno di molto più tempo per realizzarsi, così come per quelli molto piccoli. Inoltre, nel secondo caso, la forma sarebbe facilmente diversa da una sfera e complicherebbe ulteriormente le cose.

Si potrebbero, con relativa facilità, derivare le formule che descrivono il meccanismo descritto, ma penso che non sia il luogo giusto per scendere troppo nei dettagli. Basta solo riportare la relazione (approssimativa e semplificata) che ci dice in quanto tempo avviene la sincronizzazione del periodo orbitale del satellite e del suo periodo di rotazione, in funzione delle masse del pianeta (m_P) e del $satellite$ (m_S), del raggio del satellite (R_S) e, soprattutto, della distanza tra di loro (d):

t = 6 k 10¹⁰ d⁶ R_S/(m_S m_P²) anni

k è un parametro che dipende dalla rigidità del $satellite$ e varia a seconda che il corpo sia ghiacciato o roccioso. Come vedete, chi comanda veramente è al distanza che compare alla sesta potenza.

Se ci fermassimo qui, commetteremmo un grave errore di fisica. Abbiamo cambiato una rotazione, senza cambiare l’altra e nemmeno la rivoluzione. In questo modo, abbiamo ottenuto una diminuzione (o un aumento) del momento angolare totale (se avete il libro potete capire benissimo cos’è, qui non posso proseguire se no dovrei scrivere un testo completo di fisica elementare) senza fare intervenire forze esterne a quelle del sistema (la gravità e la marea risultante esistono all’interno dello stesso sistema fisico).

Questo, però, è impossibile, perché si sa benissimo che il momento angolare totale del sistema DEVE rimanere costante. Come si fa, allora, a cancellare questa mostruosità? Presto detto: si trasferisce ciò che si è guadagnato (o si è perso) in momento angolare di rivoluzione. In altre parole, se il momento angolare di rotazione diminuisce (o aumenta) si deve aumentare (o diminuire) quello di rivoluzione, allargando l’orbita del $satellite$ (oppure il viceversa), in modo che la somma rimanga costante.

Ciò è quello che è capitato alla Luna che, nata molto vicina a noi, ha raggiunto la sincronizzazione a scapito della distanza dalla Terra. Oggi la sua orbita è molto più larga di qualche miliardo di anni fa.

Però, però… sappiamo anche che essa continua ad allontanarsi. Qui le cose sembrano complicarsi. In realtà non è così. Tutto ciò che abbiamo detto per il $satellite$ vale anche per il pianeta, anche se in forma ridotta. Il pianeta subisce le conseguenze della marea del $satellite$ e si deforma in modo simile anche se meno violentemente. Tende, perciò, a rallentare (o a velocizzare) la sua rotazione. Anche la Terra lo sta facendo, benché sia troppo grande per arrivare a una sincronizzazione completa (tutti e tre i periodi perfettamente uguali tra loro). Come conseguenza, la Luna continua ad allontanarsi.

Nel Sistema Solare (a parte alcuni asteroidi) il meccanismo completo di sincronizzazione è giunto alla fine solo per Plutone e Caronte (probabilmente lo troveremo anche su altri KBO). Per loro sono uguali sia le due rotazioni che la rivoluzione. Ciò è stato possibile perché gli oggetti hanno una massa comparabile e, quindi, i tempi necessari per la sincronizzazione dei due periodi di rotazione con quello di rivoluzione sono molto simili.

Non sempre le configurazioni finali che abbiamo descritto sono quelle che si ottengono in Natura. Si possono trovare altre soluzioni di equilibrio. Una ce la mostra il piccolo Mercurio.

Quando l’orbita è eccentrica (proprio il caso del primo pianeta del Sistema Solare) e l’effetto mareale non eccessivo, si può giungere a una situazione che potremmo dire “intermedia”. Invece di una sincronizzazione, si ottiene una più complicata risonanza orbitale, chiamata risonanza spin-orbita, ossia una risonanza tra periodo di rotazione e periodo di rivoluzione. Il loro rapporto, come per le risonanze di moto medio, di cui abbiamo parlato a lungo per gli asteroidi, deve essere formato da numeri piccoli e interi. La sincronizzazione, discussa precedentemente, diventa un caso particolare di questo tipo di risonanza, quello che si ottiene per il rapporto 1:1.

Nel caso di Mercurio la risonanza è la 3:2, cioè il pianeta ruota tre volte intorno al suo asse nel tempo in cui compie due rivoluzioni intorno al Sole. Ciò implica che il giorno solare (intervallo tra due passaggi del Sole al meridiano) sia uguale esattamente a due rivoluzioni attorno al Sole. Quindi il pianeta mostra la stessa faccia al Sole ogni due anni mercuriani, come rappresentato in Fig. 5.

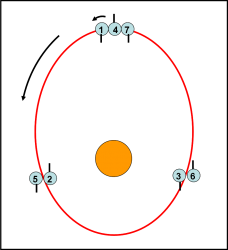
Ricordiamo che questa scoperta è stata fatta solo nel 1965 attraverso osservazioni radar. Vi sembra strano? In realtà no.  Prima si pensava che Mercurio fosse sincronizzato col Sole. Così almeno mostravano le osservazioni. Invece era solo colpa del caso, dato che il periodo di rotazione di Mercurio è esattamente la metà del suo periodo sinodico rispetto alla Terra. Ne consegue che ogni volta che il pianeta si trova nelle giuste condizioni di visibilità appare sempre nella stessa configurazione rispetto al Sole. Accidenti, veramente una bella sfortuna!

Mercurio non è nuovo a insegnarci concetti molto importanti. Pur se così piccolo è stato fondamentale per verificare la teoria della relatività. Ma questo è un discorso che affronteremo un’altra volta.

Alla prossima!