Scopriamo i misteri di Celestia & Co.

Il povero Gauss, quando ideò il metodo per calcolare l’orbita di un corpo planetario a partire da tre osservazioni, era obbligato a eseguire i calcoli a mano. Poverino! Oggi bastano pochi secondi per ottenere risultati ben più accurati e generali. Sarebbe un assurdo non utilizzare il computer che, in modo “stupido” e ripetitivo, obbedisce alle formule scritte dal loro ideatore.

Esso agisce come catalizzatore e sveltisce in modo mostruoso i tempi necessari alle capacità umane per svolgere con carta e penna calcoli anche complicatissimi. Tanto di cappello ai programmi che ormai sono alla portata di tutti, soprattutto quando le formule che nascondono sono estremamente complesse. Senza computer come si farebbe a calcolare centinaia e centinaia di modelli di evoluzione stellare cambiando, anche se di poco, i parametri di partenza? Senza di lui non basterebbe nemmeno una vita di un genio dell’astrofisica. Tuttavia, è proprio il genio (ma anche molto meno) che deve preparare il programma, se no il computer resta del tutto muto e incapace.

Questo enorme vantaggio tecnologico va sfruttato nel modo giusto. La sua vera utilità sarebbe quella di lasciare più tempo allo studioso perché si dedichi ai problemi concettuali, alle ipotesi e alle teorie e, non ultimo, alla preparazione dei programmi che lo aiutino. Tutti lavori che dovrebbero essere fatti con il cervello, un foglio e una matita. Purtroppo la comodità del computer invade spesso il campo della ricerca pura e -senza programmi già predisposti- molti si arenano, preferendo far girare per ore e ore modelli già esistenti, sperando in qualche illuminazione improbabile. La soluzione migliore è -come sempre- la giusta via di mezzo, ponderata e valutata con la mente libera. Il calcolatore è proprio quello che dice il suo nome: calcola velocemente, ma non ragiona. Questa parte è lasciata al ricercatore.

Spesso e volentieri i programmi si basano su teorie e su formule sicuramente improponibili in siti divulgativi come questo. Accettiamo quindi, in molti casi, di prendere per oro colato ciò che il web ci fornisce senza fatica. Tuttavia, quando ciò che sta dietro al computer è una formula o un algoritmo di estrema banalità, perché non cercare di spiegarlo e di farlo comprendere? Poi ognuno sceglierà se continuare a usare la “pappa pronta” o provare a compiere da solo (magari di tanto in tanto) il lavoro nascosto nella pancia del programma.

Quest’ultimo non è una lampada di Aladino che aspetta i desideri dell’appassionato per soddisfarli immediatamente. E’ spesso un procedimento che chiunque potrebbe eseguire con una semplice calcolatrice tascabile. Quanti studenti di vario livello non sanno più fare una radice quadrata con carta e penna? E quanti non faticano neanche per una moltiplicazione o una somma? Sempre di più, sicuramente, e ben vengano le piccole calcolatrici  o il computer. Ma guai se questi annullano del tutto le capacità di fare da “soli”. Ricordo un bellissimo racconto di Asimov dove in una civiltà futura si riscoprono la matematica e la geometria manuale con risvolti a dir poco inaspettati, oltre che molto divertenti.

Veniamo allora ai programmini usati molto spesso per simulare la luminosità e le dimensioni apparenti degli astri in posizioni diverse da quelle che occupano realmente. Celestia è uno di questi. I risultati sono spesso inaspettati, clamorosi e affascinanti. Un dovuto plauso a Pierluigi che li manipola con sapienza e fornisce continue sorprese. Ma è così difficile comprendere e rifare manualmente quello che fa Celestia? No, assolutamente no. Sicuramente lo può fare chiunque abbia un minimo interesse per l’astronomia (se no non frequenterebbe questo sito), gli astrofili per primi.

Cercherò allora di spiegare in modo semplicissimo il banale procedimento che sta dietro ad alcuni risultati ottenibili con Celestia e, dopo, scriverò le formule veramente infantili che possono essere usate da chiunque voglia procedere da solo e magari personalizzare la visualizzazione dei risultati.

Innanzitutto, sia Celestia che chiunque-voglia-fare-da-sè deve avere a disposizione alcuni dati di partenza. Quelli nessuno li può inventare. I dati relativi alle stelle provengono da studi lunghi, complicati, da ipotesi e verifiche, da osservazioni di livello spesso molto alto. Le caratteristiche essenziali degli astri che ci servono per simulare la loro apparenza, in condizioni a volte estreme, sono essenzialmente due: il diametro della stella e la sua luminosità, o meglio magnitudine assoluta.

Il diametro di una stella è quello che è e si conosce per un numero piuttosto ristretto di oggetti. Pochissimi sono stati misurati direttamente. La maggior parte è una stima basata sulle caratteristiche fisiche dell’astro in questione. Anche i programmi già pronti devono andare a leggere da qualche parte questi dati (anche se non ve lo dicono espressamente).  La magnitudine di un astro è invece una misura legata alla luminosità, scelta fin dall’antichità a causa delle caratteristiche dell’occhio umano. Su questo argomento non possiamo certo dilungarci ora, ma penso che tutti sappiano benissimo la differenza tra magnitudine e luminosità. D’altra parte anche Celestia la utilizza senza alcun tentennamento.

La magnitudine di una stella è una precisa indicazione della sua luminosità apparente. Purtroppo, però, la stessa magnitudine può essere data da una stella debole e vicina così come da una stella luminosa e lontana. E’ necessario sapere, allora, la distanza dell’astro per poter discriminare. Senza la distanza nel cassetto della memoria non c’è simulazione che tenga. Per tutte le stelle di cui si conosce la distanza (e sono ormai moltissime) è facile stabilire chi sia veramente tra loro più o meno intrinsecamente luminosa, ossia stabilire la magnitudine assoluta. Questa magnitudine è quella che avrebbero le stelle se fossero situate a una certa distanza, uguale per tutte. Normalmente si sceglie la distanza di 10 parsec, ricordando che un parsec equivale a 3.26 anni luce. Non chiedetemi il perché di queste scelta: basta andare a vedere alcuni metodi di calcolo delle distanze stellari… Ovviamente, bisogna avere a disposizione questo elenco di magnitudini assolute dato che nessuno se le può inventare.

Ricapitoliamo brevemente. Per compiere il lavoro di Celestia, e dei suoi fratelli e sorelle, è necessario avere sottomano gli elenchi dei diametri e delle magnitudini assolute delle stelle. Questi elenchi si trovano facilmente sia in alcuni almanacchi che sul web. Basta averli sempre accanto o crearseli cercando proprio le singole stelle su internet (soluzione migliore perché si può anche stabilire la fonte dell’informazione). Stiamo attenti ai valori dati dai programmi di cui si parla. A volte fanno medie che hanno poco senso fisico. A questo punto, siamo pronti a svelare i misteri di Celestia e di scrivere gli algoritmi che ci permettono di eseguire facilmente il suo lavoro. O, almeno, continuare a utilizzare il programma già “cotto e mangiato”, tentando, però, di capirlo.

Diametro apparente

Normalmente si usa paragonare il diametro vero delle stelle con quello del Sole, che sappiamo essere 1 391 000 km. Gli stessi elenchi dei diametri stellari forniscono spesso il diametro non in chilometri, ma in quante volte è maggiore o minore di quello del Sole, ossia danno il numero n =  D(stella)/D(Sole). Sapendo il diametro del Sole e il numero n si può facilmente risalire al diametro in chilometri della stella o viceversa.

Un’altra cosa da decidere è l’unità di misura con cui indicare il diametro apparente della stella vista in diverse posizioni. Per la nostra stella usiamo comunemente i primi d’arco. In altre parole, ciò vuol dire che un diametro di 1 391 000 km, visto a una distanza di circa 150 000 000 km (l’Unità Astronomica), sottende un certo angolo nel Cielo (diametro angolare del Sole). Per il Sole questo angolo è mediamente di 32’ 03”, ma può variare leggermente a seconda che la Terra sia al perielio o all’afelio. Per lo scopo di quest’articolo è più che sufficiente considerare un valore fisso di 32’. Ricordiamo che una circonferenza completa corrisponde a un angolo di 360 ° e che un grado si divide in 60 primi d’arco (60’) e ogni primo d’arco in 60 secondi di arco (60”). Ma queste cose un astrofilo o un semplice appassionato deve saperle per forza!

Data la distanza delle stelle e della posizione in cui vorrete metterle è, però, più utile trasformare il diametro angolare del Sole in secondi d’arco. Presto fatto: 32’ x 60 = 1920”. D’altra parte ben pochi oggetti celesti si mostrano a noi con diametri angolari maggiori di un primo d’arco. In realtà soltanto due: il Sole e la Luna. Solo in condizioni particolari anche Venere.

Lo scopo finale è, come ben sappiamo, quello di poter raffigurare nel cielo il diametro di una stella in una posizione diversa rispetto a quella che occupa abitualmente. Che cosa varierà di volta in volta? Non certo il suo diametro assoluto (che rimane sempre lo stesso), ma il suo diametro apparente, ossia il suo diametro angolare che è, come già detto, l’angolo sotteso dall’astro alla distanza scelta da noi.  Esso sarà funzione SOLTANTO della distanza cui si vorrà porre la stella, come si capisce bene dalla Fig. 1.

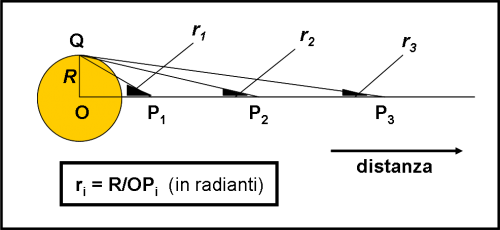
In essa la stella ha un raggio R (e, quindi, un diametro D = 2R).  Se variamo la distanza a cui la vogliamo vedere si deve cambiare la posizione del punto P (l’osservatore). Se P è più vicino il diametro angolare aumenta, se P è più lontano il diametro angolare diminuisce. Beh… è ovvio! Più siamo lontani e più piccole appaiono le cose, anche le stelle. Come si calcola il diametro angolare in funzione del punto P? Basta risolvere il triangolo OQP e ricordare la trigonometria più banale: la tangente dell’angolo marcato in neretto (ossia il diametro angolare della stella, r) vale esattamente OQ/OP, ossia R/OP.

Niente paura… abbandoniamo pure le funzioni trigonometriche se a qualcuno fanno venire l’orticaria! Dato che le distanze nell’Universo sono enormi rispetto alla grandezza degli oggetti stellari, si può procedere con una semplificazione decisiva: si assume che il diametro angolare r sia proprio OQ/OP, ossia il raggio vero della stella diviso per la distanza dell’osservatore. L’errore commesso è del tutto trascurabile, ve lo assicuro, e lo commette certamente anche Celestia.

D’altra parte l’errore dei dati sui diametri stellari è nettamente superiore alla nostra approssimazione. A causa del metodo utilizzato, la formuletta scritta nella Fig.1 esprime l’angolo in radianti. Infatti, essendo un rapporto tra segmenti non ha dimensioni. No, non spaventatevi! Un radiante è uguale a 57.2957795131 gradi. E’ quindi facilissimo passare dai radianti ai gradi e viceversa. Sapete… questi matematici fanno di tutto per complicarsi le cose. Ma a noi interessa poco. In particolare basta sapere che un radiante è uguale a 206264.81 secondi d’arco (provare per credere). Il che vuol dire che per ottenere i secondi d’arco da un valore espresso in radianti basta moltiplicarlo per questo magico numero.

Consideriamo allora il nostro amato Sole. Qual è il suo diametro angolare in secondi d’arco? Facilissimo calcolarlo (e il risultato lo sappiamo già).

D”(Sole) = 206264.81 ∙ D(km)/d(km)

Se volessimo mettere i numeri sarebbe oltremodo semplice:

D”(Sole) = 206 264.81 ∙ 1 391 000/ 149 597 887  = 1920”

Dove il diametro vero del Sole e la distanza da noi (d = 1 Unità Astronomica) sono espressi in chilometri. Il risultato è, ovviamente, 1920 secondi d’arco o, se preferite, 32 primi d’arco, come già sappiamo. Ecco allora come costruire la formula (terribile!) che usa Celestia  (e che possiamo usare anche noi a questo punto) per trovare il diametro apparente di tutte le stelle che vogliamo, poste alla distanza di 1 UA. Essa è:

D”(stella) = 1920″ n

Dove n è il numero che dice quante volte il diametro vero della stella è più grande (o più piccolo) di quello del Sole.

Se la vogliamo a distanze k volte più grandi o più piccole (sempre espresse in Unità Astronomiche) basta scrivere:

D”(stella) = 1920″ n/k

Se prendiamo il Sole, tanto per restare a casa nostra, quale sarà il suo diametro apparente se fosse messo a 10 UA (n=1, k=10)? Banale… D”(Sole) = 1920/10 = 192”, ossia 3’.2 . In questo caso, per definizione, n=1. Ovviamente, ottenevamo lo stesso risultato dividendo per 10 il diametro apparente del Sole espresso in primi d’arco…

Difficile? Non direi proprio…

E se volessimo muovere una qualsiasi altra stella? Altrettanto banale. Ad esempio, Sirio ha un diametro reale circa 3 volte quello del Sole e quindi se portata a 1 UA avrà dimensioni 3 volte quelle apparenti del Sole (n=3, k=1).  Se la vogliamo a 5 UA, dovremmo moltiplicare per 3 e dividere per 5 il diametro apparente del Sole (n=3, k=5). Tutto lì. Come vedete questo tipo di calcolo NON HA ASSOLUTAMENTE BISOGNO DELLA DISTANZA VERA DELLA STELLA, dato che la imponiamo noi dal di fuori. Mi vergogno quasi ad avere descritto un metodo così infantile…

Pari difficoltà se volessimo muovere le stelle in termini di Anni Luce. Nella formuletta originaria invece di inserire la distanza di 1 UA espressa in chilometri (circa 150 milioni), dovremmo scrivere l’Anno Luce espresso in chilometri, che corrisponde a 9 461 000 000 000  km (novemila quattrocento sessantuno miliardi di chilometri). Si ottiene:

D”(stella)= 0.”03 n/k’,

dove k’ è il numero di Anni Luce a cui si vuole portare la stella, mentre n rimane, ovviamente, sempre lo stesso. Come vedete non c’è più 1920” (il diametro apparente del Sole a 1 UA), ma 0.”03 che è il diametro apparente del Sole a un Anno Luce. Valore che si può ricavare immediatamente dalla solita formuletta che definisce il diametro angolare.

A questo punto potete fare tutte le simulazioni che volete con un compasso e un foglio. Forse impiegherete qualche secondo in più, ma saprete esattamente cosa state facendo.

Magnitudine apparente

L’unica formula che va ricordata è conosciuta sicuramente da tutti gli astrofili. Essa è quella che ci permette di passare dalla magnitudine assoluta a quella apparente di una stella:

m = M – 5 + 5 log d

Dove m è la magnitudine apparente, M la magnitudine assoluta e d la distanza della stella dall’osservatore, espressa in parsec. Questa formula potrebbe essere ricavata in modo non troppo difficile, partendo dalla formula di Pogson, che lega magnitudine e luminosità di un oggetto celeste. Tuttavia, per rimanere a livello elementare, la consideriamo come un dato di fatto, promettendo di ritornarci sopra al più presto. Per lo scopo dell’articolo è più che sufficiente accettarla come dimostrata.

Come già detto, M è un valore fisso per la stella in esame e si riferisce alla magnitudine che avrebbe se vista a 10 parsec di distanza. Il Sole, ad esempio, nella luce visibile, ha una magnitudine assoluta di 4.83 mag. La distanza della stella è la variabile su cui vogliamo lavorare. Cambiandola, si ottiene la magnitudine apparente voluta. La distanza può essere espressa in Unità Astronomiche o in Anni Luce, a patto che si divida per il numero di UA o di AL contenuti in un parsec.

In particolare, per le Unità Astronomiche, otteniamo:

m = M – 5 + 5 log (d/206000) = M – 5 + 5 log d(UA) – 5 log (206000) = M + 5 log d(UA) – 31.57

In conclusione:

m = M  + 5 log d(UA) – 31.57

Se invece volessimo lavorare con gli Anni Luce, la formula diventerebbe:

m = M + 5 log d (AL) – 7.57

A questo punto, basta inserire al posto di M il valore relativo alla stella scelta e poi cambiare la distanza a piacimento. Si ottengono facilmente le magnitudini apparenti della stella nei punti più disparati dei dintorni vicini e lontani della Terra. Un gioco da ragazzi!

Nel caso del Sole, posto dov’è ora, si avrebbe:

m = 4,83 + 5log 1(UA) – 31.57 = – 26.74, che è proprio la magnitudine apparente del Sole visto dalla Terra.

Buon divertimento!