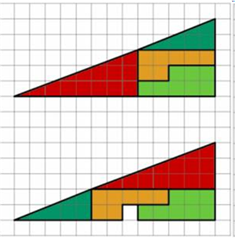
Qualsiasi superficie può essere “scomposta” in un certo numero di superfici più piccole, la cui somma deve sempre dare lo stesso risultato. Prendiamo allora un triangolo e suddividiamolo in alcune figure particolari (se volete potete anche ritagliare le varie parti), come fatto nella parte alta della figura. Rimettiamole insieme cambiandone la posizione ed ecco che nasce un vero assurdo geometrico. Otteniamo un triangolo IDENTICO a quello precedente, ma con un BUCO (un piccolo ma chiarissimo quadrato), come si vede benissimo nella parte bassa della figura. Come può essere possibile?
Vi invito a darmi la risposta. Magari è necessario uscire dalla fisica newtoniana e passare a quella relativistica. Oppure dobbiamo lavorare con i numeri immaginari e cambiare tutte le teorie odierne.
E se i buchi neri (o meglio i buchi bianchi) nascessero in questo modo? I buchi sono sempre buchi…
Attendo … celebrando il mio articolo n. 600!!

Ma chiaro, ormai è stato scoperto, quel quadrattino è il Busone di Higgs !
Premetto che non so come calcolare le superfici delle figure verde chiara e arancione. Tuttavia la superficie del triangolo originario è 32,5 (quadratini quadrati ), mentre se scompongo i due triangoli rosso e verde scuro e ne calcolo la superficie (rispettivamente 12 e 5 quadratini quadrati (!)) e le sommo alla superficie del rettangolo che è la somma delle figure verde chiara ed arancione (15 quadratini quadrati) ottengo come risultato 32. Il che conferma anche matematicamente (oltre che visivamente) la presenza di un buco bianco, ma non ne spiega la ragione.
), mentre se scompongo i due triangoli rosso e verde scuro e ne calcolo la superficie (rispettivamente 12 e 5 quadratini quadrati (!)) e le sommo alla superficie del rettangolo che è la somma delle figure verde chiara ed arancione (15 quadratini quadrati) ottengo come risultato 32. Il che conferma anche matematicamente (oltre che visivamente) la presenza di un buco bianco, ma non ne spiega la ragione.
cari tutti,
mi permetto di sintetizzare il problema (senza tanti calcoli delle superfici).
1) il triangolo completo di partenza è UGUALE a quello finale.
2) Le varie parti colorate che li compongono sono anch'esse sempre le stesse.
Eppure abbiamo creato un buco (bianco)!!!!
Comunque le due figure verde chiara ed arancione possono essere a loro volta scomposte in due rettangoli ciascuna e le loro superfici diventerebbero rispettivamente 8 e 7 quadratini quadrati, quindi non cambierebbe niente rispetto al calcolo della superficie totale. E del resto il valore delle superfici dei due triangolini non può cambiare dalla prima alla seconda figura, quindi perché il valore della superficie del triangolo "padre" non corrisponde a quello della somma dei suoi "figlioletti"?

Mi rendo conto di avere fatto ragionamenti per poi tornare alla domanda di Enzo, quindi non ho concluso niente :facepalm:
P.S.: secondo me bisogna introdurre lo smiley del facepalm.
P.P.S.: complimenti per i 600 articoli!!!
il primo non è un triangolo è un quadrilatero basta guardare le 2 pendenze diverse che si trovano in zona "ipotenusa"
Caro Enzo,

congratulazioni per i primi 600 articoli... noi aspettiamo di leggere, sempre con grande piacere, i prossimi 6000...
Ma per me è solo un'illusione ottica, un riflesso condizionato. Le superfici delle due figure sono uguali, ma la seconda figura non è un triangolo. Il quadratino bianco è esterno sia alla prima che alla seconda figura...
non capisco bene cosa vuoi dire... scusa!
Un consiglio: provate a ritagliare le figure colorate dalla Figura in alto e poi rimettetele insieme e vedete se riuscite a creare la Figura in basso. Così si eliminano tutti gli effetti ottici (supposti)...
Ovviamente non darò la soluzione fino a quando non ci sarà un bell'elenco di risposte...
non capisco bene cosa vuoi dire... scusa!
Nemmeno io... è proprio un bel rompicapo!
Vediamo...
Le due aree (5.12/2 quadratini) sono uguali. Le due figure irregolari (verde + chiaro) sono uguali: rispettivamente 7 e 8 quadratini.
Il quadratino bianco della seconda figura, non può che essere pari ad una minore dimensione dei triangoli rosso e verde.
Perché succede questo? Magia!!!