Non vi deve essere alcuna paura ad ammettere i propri limiti riguardo a certi concetti. Io per primo, molto probabilmente, non sono stato in grado di spiegarlo nel modo migliore. Qui non si pontifica, ma si cerca di spiegare e di accettare ogni miglioramento atto a perfezionare l’argomento trattato. Uno per tutti e tutti per uno!
Il cono di luce è troppo importante per comprendere e soprattutto descrivere in modo relativamente semplice lo Spazio-Tempo e molti fenomeni o situazioni ad esso collegate. Devo perciò tentare, nei miei limiti, di tornarci sopra e cercare di renderlo cosa ovvia e intuitiva da utilizzare normalmente. Sappiamo che è una rappresentazione limitata, incompleta, a volte ambigua, ma vi assicuro che è la più semplice e generale per spiegare e partecipare in prima persona ai fenomeni dell’Universo. Ne abbiamo già parlato, discusso. Lo abbiamo costruito e usato. Ma per non farvi saltare avanti e indietro nell’archivio, penso che sia meglio spiegarlo nuovamente partendo dall’inizio. Poi, se tutto sarà compreso, tornate agli articoli precedenti e probabilmente li comprenderete meglio. In caso contrario, ditemelo subito! Come dice il titolo: DOBBIAMO CAPIRLO. E sono sicuro che tutti i lettori ci possono tranquillamente riuscire. Basta avere pazienza.
Bando alle ciance e cominciamo.
Definiamo lo Spazio-Tempo come un sistema di riferimento a due dimensioni. La prima coordinata (asse orizzontale) è lo Spazio, la seconda (asse verticale) è il Tempo. Abbiamo duramente semplificato la realtà, in quanto invece di utilizzare le tre dimensioni dello Spazio ne abbiamo usato una sola. Con un po’ di immaginazione potremmo anche usare due dimensioni (come nei dipinti egiziani) e si riuscirebbe ancora a disegnare (anche se poi le cose si vedrebbero meno chiaramente).
Nel secondo caso, lo Spazio sarebbe rappresentato dal piano perpendicolare al foglio (due dimensioni appunto) e il tempo rimarrebbe l’asse verticale. La Fig. 1 descrive quanto detto:
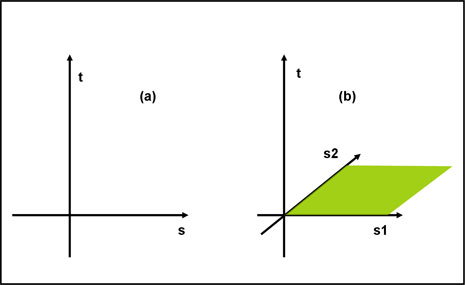
Figura 1. Il sistema di riferimento (a) ha due sole dimensioni: lo Spazio è l’asse orizzontale e il Tempo l’asse verticale. Il sistema (b) a tre dimensioni è più vicino alla realtà di tutti i giorni: gli assi s1 e s2 definiscono lo Spazio, mentre il Tempo è sempre descritto dall’asse verticale
Nel caso (a) tutto ciò che esiste può muoversi nello Spazio solo lungo la linea s; nel caso (b) solo nel piano s1- s2. Sono entrambe limitazioni di ciò che ci circonda, dato che il movimento spaziale può avvenire lungo tre dimensioni (lunghezza, larghezza e $altezza$). Se, però, volessimo questa rappresentazione non sapremmo più dove disegnare il Tempo. Visto che dobbiamo semplificare la realtà, tanto vale usare la rappresentazione (a) che ci dà minori problemi nei disegni. Immagineremo di poterci muovere solo lungo una linea… pazienza! Un piccolo sforzo di fantasia…
A questo punto introduciamo la Fig. 2, dove vogliamo vedere, nella rappresentazione (a) della Fig. 1, quali sono le possibilità di movimento nello Spazio-Tempo definito dalle due coordinate s e t.

Figura 2
Limitiamoci a considerare i due assi s e t (lo Spazio e il Tempo) e mettiamoci nell’origine degli assi, nel punto T. Cosa rappresenta il punto T ? La nostra posizione nello spazio e nel tempo, OGGI. In altre parole, abbiamo considerato OGGI come l’origine dello Spazio e del Tempo (potevamo cambiare origine, ma questa scelta ci fa abbastanza comodo, per adesso).
Cosa rappresenta la linea blu? Essa descrive per ogni istante t la nostra posizione nello Spazio s. Quella sotto il punto T (OGGI) descrive il nostro passato. Quella sopra rappresenta il nostro futuro. Ho disegnato una linea a caso, ma potevo cambiarla e renderla più o meno complicata. Una cosa sicuramente NON potevo fare: tornare indietro! In questo caso avremmo viaggiato nel passato e questo è impossibile.
La nostra linea di esistenza può andare solo verso l’alto, senza ripensamenti, pur muovendosi verso sinistra o destra. La maggiore o minore pendenza della linea blu ci indica anche quanto siamo andati e andremo veloci (Spazio percorso nell’unità di Tempo). Ad esempio, se non ci fossimo mai mossi e non ci muovessimo mai in futuro, quale sarebbe la nostra linea di esistenza? Facilissimo. Non essendoci mai mossi nello Spazio, ma solo nel Tempo, avremmo descritto esattamente l’asse verticale, quello del Tempo.
Possiamo muoverci a piacere verso sinistra o verso destra? Teoricamente sì, ma non potremmo farlo troppo velocemente. Perché? Dobbiamo seguire le regole della relatività del caro amico Einstein e quindi NON POSSIAMO SUPERARE LA VELOCITA’ DELLA LUCE.
Quale sarà allora il limite del nostro spostamento? Proprio la linea seguita da un corpo che va alla velocità della luce. Questa linea la disegniamo come una retta che passa per T e forma un angolo di 45° rispetto all’asse dello Spazio s (e quindi anche con l’asse del Tempo t). In realtà ne possiamo disegnare due, una che va verso sinistra e una che va verso destra. Ed ecco costruito facilmente il doppio triangolo colorato in rosso. L’angolo di 45° è stato scelto così per valide ragioni legate alla teoria che sta dietro a questa trattazione, solo apparentemente semplice. A noi, comunque interessa poco. E’ un limite come un altro. Potevamo anche stringere o allargare le due rette. Voleva dire solo cambiare l’unità di misura dello Spazio e del Tempo.
45° vuole, però, proprio dire che nell’unità di Tempo (ad esempio l’anno) la luce percorre nello Spazio esattamente un anno luce. In altre parole ancora, se un centimetro dell’asse t vale un anno, un centimetro nell’asse s vale proprio 9,461∙1012 km, ossia 9461 miliardi di chilometri, proprio lo spazio percorso dalla luce in un anno. Ma non complichiamoci inutilmente le cose…
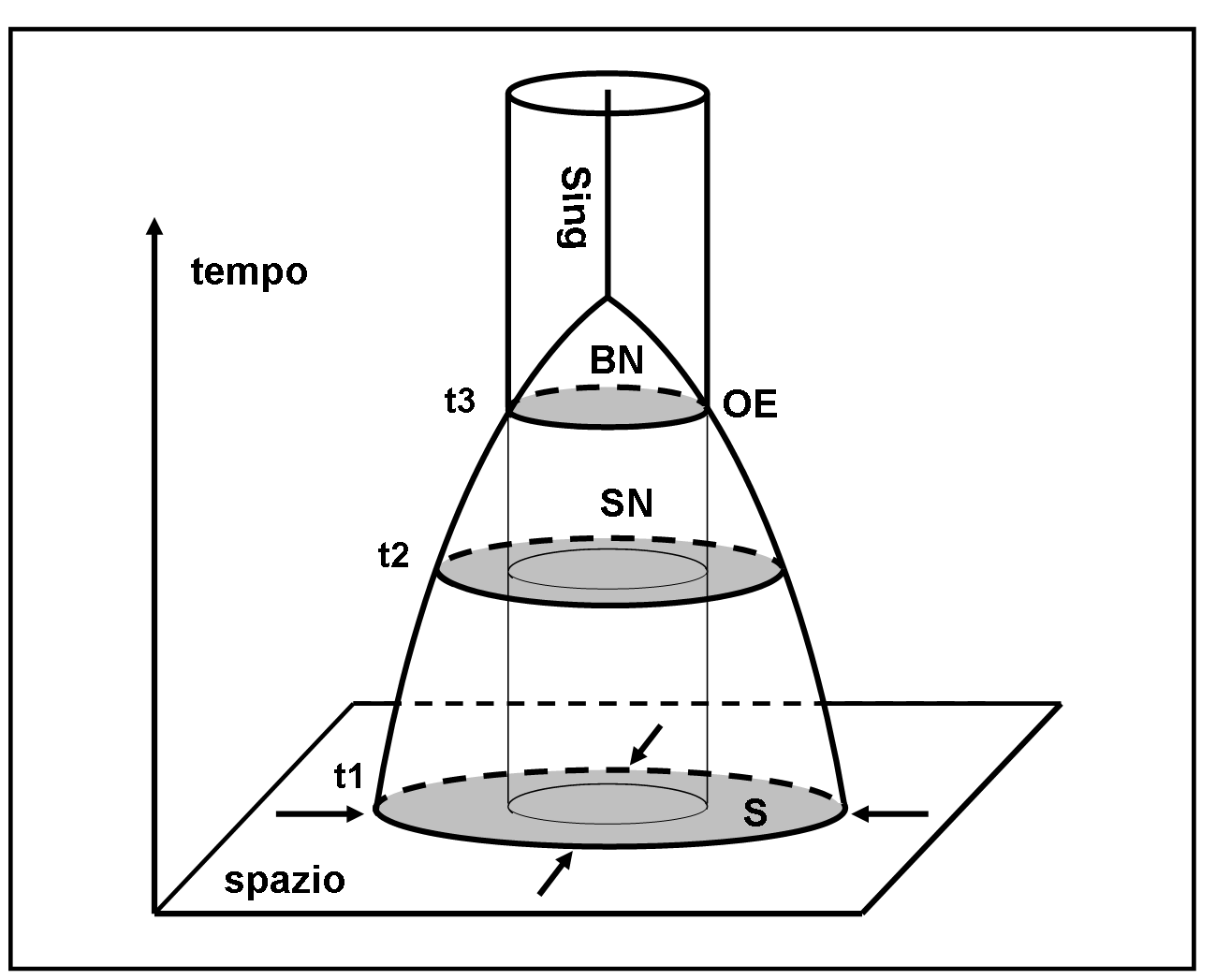
I due triangoli rossi formano il cono di luce dell’oggetto T all’istante t = OGGI. Ovviamente se cambiassimo origine degli assi si sposterebbe anche il cono di luce, ma sempre parallelamente a se stesso (non può certo ruotare). La Fig. 3 ci mostra alcuni coni di luce relativi a punti del nostro passato e del nostro futuro.
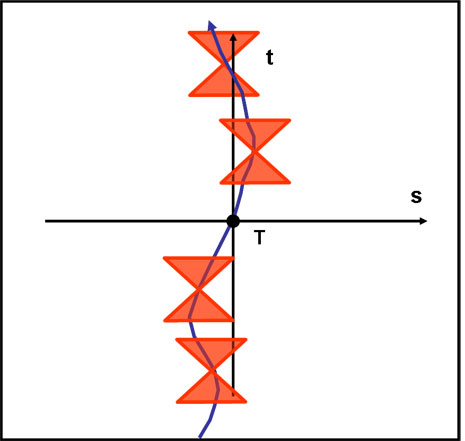
Figura 3
Alcune considerazioni molto importanti.
I coni di luce non sono limitati dalla forma a “farfallino” che ho disegnato. Ognuno di essi prosegue all’infinito verso l’alto e verso il basso. Se l’avessi disegnati così, però, avremmo avuto troppe linee tra i piedi. Fate questo esercizio da soli e vedrete (come deve essere) che ognuno di essi conterrà sempre tutta la linea blu. E’ un caso? Assolutamente no! Devono sempre contenerla dato che essa rappresenta la posizione dello Spazio-tempo del punto T durante la sua esistenza e quindi deve fare sempre parte di qualsiasi cono di luce (passato o futuro) del punto T. Se la curva uscisse fuori vorrebbe dire che si è superata la velocità della luce e questo non è possibile.
Perché li chiamiamo coni di luce? Per capirlo facilmente basta tornare alla Fig. 1 e considerare la rappresentazione (b). In uno spazio a due dimensioni il “farfallino” diventa proprio un cono (rotazione della retta limite attorno all’asse del Tempo). Rappresentiamolo nella Fig. 4.
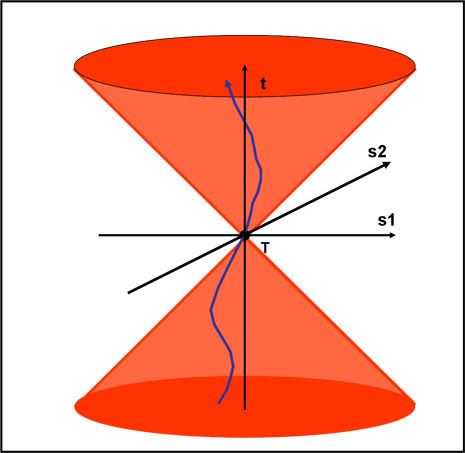
Figura 4
Il “farfallino” nasce come intersezione del cono vero e proprio con il piano del disegno. Tutto lì. La rappresentazione si semplifica, ma i concetti restano immutati. Basta pensare in termini di uno Spazio a una sola dimensione, come il Tempo…
Come potremo allora definire il cono di luce di un certo oggetto (o se volete di un certo evento)? Esso è l’insieme delle posizioni che un oggetto può assumere nel suo futuro e che ha potuto assumere nel suo passato. Un oggetto fermo nello Spazio descrive perfettamente l’asse del Tempo (nello Spazio si può stare fermi, nel Tempo no…). Un corpo che viaggia alla velocità della luce descrive esattamente il bordo del cono di luce (si chiama così proprio per questa ragione…). Se l’oggetto che vogliamo considerare fosse una lampadina che s’accende o una stella che nasce, la luce che emette è rappresentata nel futuro proprio dalle rette che limitano il suo cono di luce. In altre parole, i fotoni che nascono dall’oggetto in questione, descrivono i bordi del cono di luce. Ancora meglio, per rappresentare la luce che invia una stella nello spazio, basta disegnare le rette che limitano il cono di luce della stella. Come sarà utile in seguito!
Domanda terribile, ma estremamente utile: “Cosa esiste al di fuori del “nostro” cono di luce?”. Il nulla. Ossia tutto ciò che non potremmo mai conoscere e che mai abbiamo conosciuto.
Un po’ di esempi.
Esiste il cono di luce del Big Bang. Sicuramente sì. Esso altro non è che tutto ciò che si è originato dal Big Bang. In altre parole, rappresenta le posizioni che ha assunto, assume e assumerà tutto ciò che lo costituiva. Tenendo conto che dentro al Big Bang vi era il TUTTO, la frase precedente dice semplicemente che il cono di luce del Big Bang è l’intero Universo. Mica male eh?!
Esiste un cono di luce passato del Big Bang? NO. A meno che non esistesse qualcosa che abbia dato origine al Big Bang.
Questo sembrerebbe il modo migliore per descrivere l’Universo. Il cono di luce che parte proprio dal punto che ha le coordinate di Tempo e Spazio uguali a ZERO (prima non esisteva né uno né l’altro). In realtà molti lo fanno, ma bisogna entrare in un’ottica non certamente ovvia e nemmeno facilmente rappresentabile su un foglio. Vogliamo provare? Ecco, allora la Fig. 5, che descrive appunto tutto lo Spazio-Tempo dell’Universo.
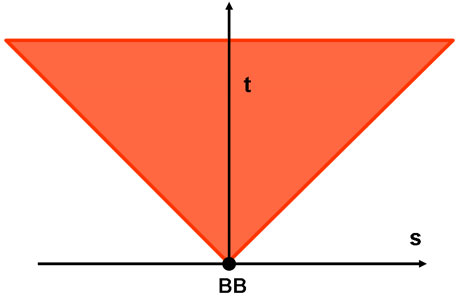
Figura 5
E’ stato facilissimo. Oltretutto abbiamo anche eliminato la parte del “passato”, dato che non esiste. Perché allora non usiamo sempre questa banalissima figura? Presto detto: “Ci porterebbe a situazioni insostenibili e non disegnabili”. Fatemi fare alcuni esempi. Se tutto nasce dal Big Bang, è facile descrivere il futuro delle stelle o delle galassie o dei pianeti che nascono da lui. Lasciamo perdere i movimenti propri degli oggetti e vediamo solo il movimento che essi hanno per effetto dell’espansione dell’Universo. A ogni oggetto è associabile una linea di esistenza che possiamo far nascere tranquillamente dal Big Bang. Prima che nascesse effettivamente la stella o la galassia o il pianeta, vi erano le particelle elementari che li avrebbero formati e quindi possiamo considerare che ogni oggetto nasca sempre dal Big Bang. L’insieme di queste rette di esistenza sono rappresentate in Fig. 6.
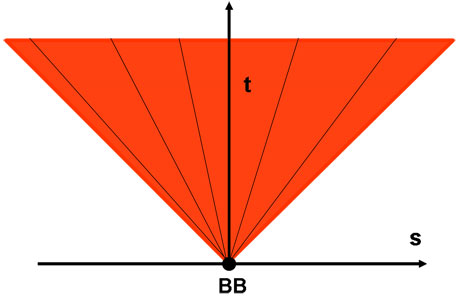
Figura 6
Magnifico! Possiamo disegnare tutti gli oggetti che vogliamo. A un certo punto, lungo le linee, si accendono le stelle e gli altri oggetti celesti, che poi seguono l’espansione dell’Universo: a mano a mano che il Tempo passa, si allarga, infatti, lo Spazio. Tutto perfetto allora? Assolutamente no!
Innanzitutto, cosa vi è al di fuori del cono? In questo caso proprio il NULLA. Non il “nostro” nulla, ma il vero nulla. Eppure siamo riusciti a disegnarlo e -se volessimo- disegnarci sopra qualcosa (teoricamente e praticamente impossibile).
Vi è di peggio, però. Facciamo nascere una stella S lungo una certa linea di esistenza. Automaticamente essa ha anche un suo cono di luce che, ripetiamo, rappresenta tutte le possibili posizioni che la materia di cui è composta ha potuto assumere nel passato e assumerà nel futuro. Possiamo e dobbiamo farlo, se no è impossibile descrivere le relazioni tra i vari oggetti dell’Universo o quanto meno descrivere le traiettorie della luce che ognuno di loro emette.
Proviamo a disegnarne qualcuno? Poveri noi… La Fig. 7 ci mette nei guai.
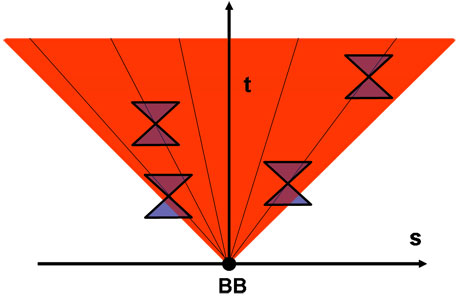
Figura 7
Va ancora tutto bene per i coni di luce futuri dato che restano sempre compresi dentro al cono di luce del Big Bang (come DEVE essere, se fanno parte dell’Universo). Ma quelli passati sono incontrollabili! Essi dimostrano di aver viaggiato al di fuori del cono di luce del Big Bang, ossia nel NULLA. No, questo non ha senso. La figura potrebbe anche essere mantenuta, ma bisognerebbe deformare la forma dei coni di luce mano a mano che si va verso i bordi. Insomma un enorme pasticcio che ci complicherebbe le cose in modo mostruoso.
Dobbiamo, allora, cambiare un poco la forma del nostro disegno. Peccato: in fondo era bello vedere disegnato il punto Big Bang e il TUTTO che nasceva da lui. Accidenti alle nostre limitazioni grafiche!
Abbiamo due alternative. O manteniamo la forma dei coni di luce e deformiamo lo Spazio-Tempo, oppure consideriamo uno Spazio-Tempo ancora più realistico (senza rappresentare quel fastidioso NULLA, ad esempio) e deformiamo un poco i coni di luce.
Proviamo con la prima possibilità. Per mantenere la forma dei singoli coni di luce, dobbiamo per forza trasformare il punto Big Bang in una retta infinita, quella dello Spazio, al tempo ZERO. Solo così ogni cosa nel suo passato finirà in quel fatidico “punto”. Ed ecco la Fig. 8.
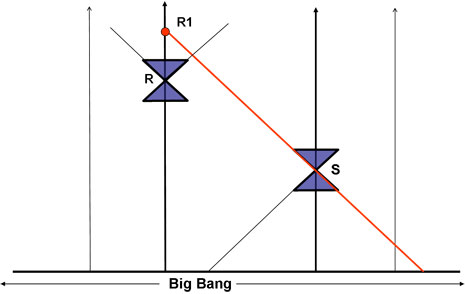
Figura 8
Mica male, eh?! In fondo basta aver fantasia e immaginare il punto Big Bang come una retta. Poi tutto il resto sembra filare perfettamente. Ad esempio la luce emessa dalla stella S raggiungerà la stella R nel punto R1. E non dobbiamo disegnare curve strane. Questa rappresentazione ci dimostra anche che nel passato di ogni oggetto celeste esiste il Big Bang e che, di conseguenza, il Big Bang è visibile dappertutto, basta guardare nel proprio passato.
In realtà, queste figure le avevo già utilizzate tempo fa per dimostrare perché il Big Bang si dovrebbe vedere dappertutto (andate a recuperare quei vecchi articoli e magari adesso vi sembreranno più semplici…).
Tuttavia, sorge un grave problema descrittivo: “L’Universo non si sta espandendo!”. Accidenti è vero. In realtà, potrei introdurre l’espansione attraverso un cambiamento di coordinate (le cosiddette coordinate co-moventi), ma complicherei sicuramente la visione immediata. Malgrado la Fig. 8 sia forse la migliore di tutte (a parte piccole deformazioni che bisognerebbe aggiungere) non risulta così comprensibile e ovvia per un lettore non troppo smaliziato.
Non ci resta che fare una cosa. Tornare al caro e vecchio palloncino che si gonfia al passare del tempo, ossia alla rappresentazione che abbiamo usato frequentemente negli ultimi articoli sullo Spazio-Tempo.
In questo modo vediamo il Big Bang come un punto, non vediamo il nulla, ma soprattutto vediamo molto bene l’espansione dell’Universo. Bisogna però adottare delle deformazioni non molto difficili.
Innanzitutto lo Spazio non è più rappresentato da una retta, ma da una circonferenza che aumenta le sue dimensioni con il passare del tempo. Anzi, il cui raggio è proprio il tempo passato a partire dal Big Bang. Poi dobbiamo deformare i coni di luce. In che modo? Presto detto: “Devono contenere tutti il Big Bang”. Ciò vuol solo dire che nel loro passato devono diventare un punto quando giungono a lui. Tutto il resto rimane invariato a parte la loro forma un po’ strana.
Le curve limite sono sempre quelle percorse dalla luce e si incrociano nel punto che rappresenta l’oggetto al tempo prescelto. Ecco finalmente la rappresentazione ben conosciuta, disegnata in Fig. 9
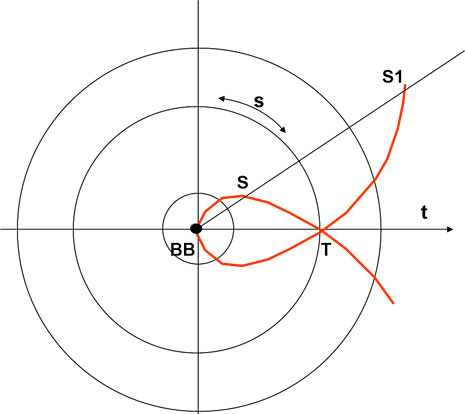
Figura 9
Il Tempo si misura lungo gli assi che partono dal centro e lo Spazio lungo le circonferenze che si allargano a mano a mano che cresce il tempo. Il cono di luce di T si deforma secondo le linee rosse. In T vediamo tutta la luce che sta sul nostro cono di luce passato (quindi, ad esempio, quella della stella S) mentre, ad esempio, la nostra sarà vista dalla stella S quando essa arriverà in S1.
le linee rosse indicano infatti il percorso spazio-temporale della luce. Per costruire esattamente (o quasi) il cono di luce basta seguire le istruzioni riportate in questo recente articolo.
Tra parentesi, variando la velocità della luce, si ottengono proprio i casi limite descritti nella parte finale di questo articolo
Sono stato abbastanza semplice? Spero di sì. Comunque, dateci dentro e ditemi se e dove devo chiarire ancora meglio le cose… il cono di luce DEVE essere capito! Nel frattempo, mi scuso con chi invece aveva già compreso tutto. Prendetelo come un ripasso. Serve anche a me…


Ok, la cosa mi si sta schiarendo, ma nelle altre rappresentazioni la parte esistente era evidenziata con un colore, in questa quale sarebbe, sempre quella compresa tra le linee?
Grazie Enzo per la bella domenica passata a PROVARE a capire l’intera faccenda con i figli; comunque sia, mi sono divertito moltissimo ed è pure sorta una questione nuova: alla metafora del palloncino ho detto di immaginare il tessuto spazio-tempo come la gomma del palloncino e tutto ciò che vediamo (galassie, luce, energia, insomma tutta la parte visibile o comunque percepibile e fino alla nostra terra e quindi a noi stessi) come la patina lasciata dal pennarello usato per disegnare il tutto. – Ma allora papà, ci stiamo allargando pure noi?- Riuscendo a malapena a nascondere l’imbarazzo ho risposto di si, solo che non possiamo accorgercene perchè si allarga anche il metro….AIUTO!!!!!!!!!!!!!!
caro Roberto th,
disegnare col palloncino porta inevitabilmente a questo controsenso… Il fatto è che le masse che popolano l’Universo creano distorioni nello spazio-tempo, ma non sono lo spazio-tempo. Ne sono abitantii. Quando si gonfia il palloncino si gonfia solo il tessuto spazio-temporale, ma non gli abitanti. Dovremmo immaginare punti sul palloncino che non seguono la sua dilatazione, ma restano sempre uguali come dimensioni. E quindi anche le loro deformazioni rimangono circoscritte. Tuttavia, la tua risposta è -in qualche modo- affascinante e -in fondo- avvicina al problema dei viaggi a velocià prossime a quella della luce. Rallentano gli orologi per chi sta fuori e altre cose, ma per noi che siamo in viaggio tutto resta come prima…
Io ti consiglierei di dire che le galassie, le stelle, ecc. non sono disegnate sul palloncino, ma sono attaccate con la colla e quindi le loro dimensioni non cambiano gonfiando il palloncino, ma le loro distanze reciproche sì…
Vedrai che capiranno…. In ogni caso tutta la mia stima per te e la tua splendida famiglia… 😛 Uno speciale augurio a tutti voi…
scusa Vojager, puoi chiarirti meglio? Cosa intendi per “parte esistente”? Se è il nostro futuro è proprio evidenziata dal colore…
Era ora! Cosa posso dire, grazie Pierluigi! 😉
@enzo
quello che intendo è che ad esempio nella figura 5 si nota il cono che parte dal big bang e che si espande su una superfice colorata di rosso. Come mi sembra di capire quella superfice rappresenta l’universo ossia tutto ciò che c’è e al di fuori di quella superfice non ci può essere niente perchè non esiste.
Nella figura nove cambia la raffigurazione delle coordinate e non riesco a capire dove trovare la corrispondenza alla superfice colorata della figura 5, ossia tutto ciò che è.
Magari potrei anche sbagliarmi a pensarla in questi termini, non so, mi si sta complicando la comprensione però mi piacerebbe tanto capire.
Grazie per la vostra pazienza
Caro Enzo,
il cono penso di averlo capito (grazie a te 🙂 ) un pò meno la figura “9”, però adesso mi vorrei concentrare sulla figure 7 e 8. La figura 7 è molto intuitiva, il problema grafico che si presenta potrebbe essere legato alla velocità del tempo in funzione della gravità e quindi l’asse tempo dovrebbe avere una scala decrescente? Enzo non so se sono riusito a spiegarmi e se ho detto cose che hanno senso. Ti ringrazio comunque per la tua grande pazienza 😥 😉
Grazie di cuore, ma qual’è la differenza tra “abitante luce” che sappiamo allungare la sua onda nel suo viaggio attraverso le trame dello spazio-tempo e “abitante umano”? Forse che luce, proprio perchè molto veloce, attraversa innumerevoli di queste “trame” che la stirano nell’effetto redshift, mentre noi, immobili nel nostro sistema di riferimento, non subiamo questo effetto, se non in modo impercettibile?
Permettimi di contraccambiare gli auguri con l’auspicio dell’arrivo di un’onda luminosa del più intenso rosso possibile.
caro gaetano,
hai perfettamente ragione sulla variazione del tempo di cui non ho parlato per non complicare ulteriormente le cose. Se vai negli articoli citati in basso, vedrai che è stata inserita proprio dove te la saresti aspettata. Diciamo che questo articolo vuole essere un’introduzione per partire con il piede giusto per quelli passati… Insomma, ho fatto il contrario… Pardon 😳
caro raffaele,
se ho bencapito ciò che dici, posso risponderti che è la luce a “stirarsi” e non i corpi solidi. Anche la nostra luce riflessa che si perde nello spazio subirà lo stesso stiramento. Così come non è la stella che emette la luce a stirarsi, ma solo la luce emessa da lei.
caro Vojager,
ti spiego facilmente. Nella Fig. 8 lo spazio esistente è tutta la figura e quindi non ho più bisogno di colorarla per metterla in evidenza. E’ come se avessi “stirato” il triangolo in modo da farlo concidere con tutto il piano della figura (per farlo è necessario cambiare le coordinate…). Nell’ultima figura, tutto lo spazio-tempo è rappresentato dal cerchio che si allarga (il raggio è il tempo e la circonferenza è lo spazio). Il cono di luce indica soltanto quello che possiamo vedere noi, ossia l’insieme di tutti gli oggetti dello spazio-tempo la cui luce è riuscita a raggiungerci. Gli oggetti che stanno fuori non esistono per noi, solo perchè la loro luce non è ancora arrivata fino a noi. OK? Comunque, insisti pure… 😛
Sto studiando, eh, un po’ alla volta…però comincio a dipanare dubbi e schiarire le idee…
Ma scusate, la figura 7 non è tanto incoerente. XD basta solo mettere in prospettiva in modo appropriato i coni di luce. La quarta dimensione sarebbe rappresentata dalla deformazione del cono di luce. Il cono di luce si restringe con l’avvicinarsi al big bang, perchè ogni retta parte da lui! (e quindi, ogni cono dello spazio e del tempo deve deformarsi pur mantenendosi parallelo alla linea del tempo orizzontale) Questo spettro dimostrerebbe che nessuna luce potrebbe arrivare ad uscire nel nulla (perchè nel nulla nulla cè e quindi manco esisterebbe.. fino a prova contraria il nulla non esiste) e che tutto cio che conosciamo compreso il big bang potrebbe arrivare ad avere anche un passato. Con lo spettro in prospettiva non si dovrebbero usarne altri e si potrebbe pure calcolare la velocita’ della luce delle stelle in passato che (seppur velocita’ della luce) era diversa da quella di oggi.
link: http://img407.imageshack.us/img407/7342/54957197.jpg
caro Martino,
quello che proponi tu è proprio quello che troverai in uno degli articoli che avevo scritto tempo fa. Resta comunque il nulla al di fuori del cono di luce del Big Bang, che è meno intuitivo dell’ultima versione. questione di scelte… Comunque sono solo approssimazioni..
secondo me con questo spettro si percepisce come mai gli oggetti nel passato rallentano visibilmente e come mai le loro velocita’ calcolate con la nostra velocita’ della luce raggiungono numeri elevatissimi. potrebbe trattarsi di un semplice errore di calcolo, nel senso che noi usiamo i nostri punti di riferimento e i nostri numeri che invece sono piu’ simili alla realta’ lontana che non riusciamo a percepire.
Se questo fosse vero quindi si potrebbe anche dire che il tempo è lo stesso dappertutto ma che a deformare le realta’ e le dimensioni è lo spazio attorno in cui ci troviamo, e forse, la stessa forma dell’universo che come una lente o l’interno di un vetro cristallizzato distorce le dimensioni insieme alle velocita’ (che per noi appaiono elevatissime in realta’ sono le stesse). Giove ad esempio avrebbe un moto di rivoluzione enorme, ma non è una trottola XD non potrebbe mai trasformarsi in un tornado, perchè appunto è un pianeta compatto. La sua velocita’ elevata in numero è solo frutto della sua enorme dimensione (piu che risultato è una conseguenza).
enzo: si si mi ricordo che lo avevevate scritto quell’articolo sulla velocita’ della luce.
Martino… no, io intendevo quello sul Big Bang dappertutto, come segnalato in fondo all’articolo qua sopra… Penso nelle conclusioni… se ricordo bene.
Il cono di luce, con tutte le sue possibili interpretazioni ed utilità, è una delle cose più intriganti che riguardano l’astrofisica. La trasformazione del cono di luce del big bang in coordinate sferiche poi è stato uno degli argomenti trattati in passato che più mi ha coinvolto, soprattutto nei commenti dell’ articolo “universo e universo osservabile”, che ancora ricordo a menadito.
Un caloroso saluto a tutti quindi, in particolare ad Enzo, che quando tratta questi argomenti mi manda completamente in brodo di giuggiole!
Si ho riletto tutti e tre gli articoli. Ma allora se quello che non vediamo nel cono di luce sta vicino a noi piu di qualsiasi altro oggetto, come mai non riusciamo a vederlo? Allora il cono di luce è la prova che esistono dimensioni/universi paralleli tanto citati?! Ma come è possibile non vedere un oggetto celeste che è anche piu’ vicino a noi (sulla stessa linea del tempo) non si spiega.. O_O forse la linea tiene solo conto della nostra realta’ o gravita’ fino a prova contraria se un oggetto passa accanto alla terra lo vediamo in tempo reale, no?
caro Martino…
temo che tu stia facendo un po’ di confusione. Un oggetto che è vicino a noi sulla linea del tempo non è assolutamente un oggetto vicino. Ricordati sempre: lo spazio si misura lungo le circonferenze o le rette orizzontali. Non si può misurare lungo l’asse del tempo…quello è , appunto, l’asse del tempo non dello spazio. Rileggi bene passo passo…
Gentilissimo Enzo insisto.
Ok, la circonferenza che si espande rappresenta lo spazio nella sua espansione nel tempo e quest’ultimo è rappresentato dal raggio.
Quindi ci sarà un’area che noi possiamo percepire ed una che non percepiremo mai per ovvi motivi spazio-temporali.
L’area che percepiamo è possibile colorarla? Oppure questa mia richiesta denota che ancora non riesco a capire tutta la questione?
Grazie
caro Vojager,
l’area che percepiamo attraverso la luce che ci invia è la superficie del cono di luce (deformato o no che sia). La sua sezione sul piano del foglio sono le due linee curve nel caso del palloncino che si espande. Volendo, potrei colorare la sua parte interna, ma potrebbe creare problemi, perchè quello che vi è nel suo interno (nel piano del foglio) ci ha già raggiunto in passato e non ci raggiungerà più (inteso come luce, ovviamente).
Spett. Staff,
io so che esitono corpi celesti che non possono essere visibili dalla Terra nè oggi nè mai. La fig. 9, che ho visto anche in altri articoli, esemplifica bene questo concetto: in pratica se la retta “tempo” di S formasse un angolo >= 45 gradi con la retta “tempo” di T, la luce di S non arriverebbe mai ad intersecare la retta “tempo” di T stessa.
Nelle figure 7 e 8 questo fatto non è così apparente: ogni cono di luce sembra intersecare o aver intersecato ogni altro cono. Come si può rappresentare l’inosservabilità tra due corpi celesti secondo gli schemi 7 e 8?
Spero che la mia domanda sia almeno plausibile. Ringrazio in anticipo.
caro Rodolfo,
perfettamente plausibile la tua domanda. Tuttavia, proprio la Fig. 8, che descrive il Big Bang come una retta infinita all’istante 0 è quella che meglio esemplifica l’inosservabilità. In essa sono considerate le coordinate comoventi e quindi non si può vedere direttamente l’espandersi dello Spazio-Tempo. Tuttavia, pensa di andare molto lontano sia a destra che a sinistra. In quel punto fai partire il tuo cono di luce. Se la distanza iniziale tra questa sorgente e la Terra è molto lontana, prima che il suo cono di luce raggiunga la nostra linea di esistenzza l’Universo potrebbe anche non esistere più. Proprio le dimensioni praticamente infinite della retta del Big Bang possono permettere di assumere due oggetti a distanza pressochè infinita tra loro tale che i coni di luce non si intersechino mai.
Se non ti convince dimmelo… mi raccomando! 😉