Consideriamo il Sole come una sfera (incandescente) avente il raggio pari a 696000 Km (ben 109 volte il raggio dell Terra). E’ abbastanza immediato renderci conto che guardandola da un certo punto, questa sfera è vista sotto un certo angolo. Quanto più ci allontaniamo, tanto più piccola ci appare la sfera e minore sarà l’angolo sotteso. Viceversa se ci avviciniamo alla sfera, la vediamo ovviamente più grande, con un angolo maggiore.
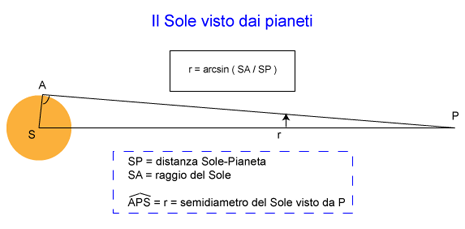
Per capire di quanto cambia l’angolo di visuale della sfera del Sole, in base alla distanza da cui guardiamo la sfera stessa, ci viene incontro la trigonometria, con una formuletta facile facile. Guardando la figura, S è il centro del Sole, P è il nostro punto di osservazione: la sfera, con centro in S, sottende l’angolo APS, cioè viene vista con un angolo che in astronomia si chiama semidiametro apparente (meno comunemente “raggio apparente”).
Se consideriamo la Terra nel punto P, abbiamo che il lato SP è pari alla distanza Terra-Sole (prendiamo un valore medio, facile da ricordare, 150 milioni di Km), dunque sostituendo i valori, otteniamo un valore per r pari a circa 0.265 gradi, che diviso 60, dà il valore di circa 16′ (primi di grado).
Dunque il Sole, visto dalla Terra, sottende un angolo pari al doppio del valore trovato (il diametro apparente) e cioè 32′, qualcosina in più di mezzo grado: facendo calcoli analoghi per la Luna, cioè prendendo per SA il valore 1738 Km e per la distanza SP il valore 384400 Km, otteniamo alla fine un angolo r molto vicino al precedente, con un semidiametro anche in questo caso pari a circa 32′.
Questo è un fatto molto importante: la Luna e il Sole osservati dalla Terra (pur essendo a distanze enormemente differenti) vengono visti sotto un angolo molto simile, variabile in funzione della distanza della Terra dal Sole e della Luna dalla Terra. Questa notevole coincidenza comporta il verificarsi sulla Terra di uno dei fenomeni astronomici più spettacolari: le eclissi di sole!
Tornando ai pianeti, è lecito attendersi che dal pianeta più vicino, Mercurio, il Sole appaia più grande (e caloroso, ovviamente), mentre mano a mano che ci si allontana verso i pianeti gassosi fino ad arrivare al “pianeta nano” Plutone, l’angolo sotteso è sempre più piccolo. Ecco che dunque possiamo ottenere il raggio del Sole, visto da un qualsiasi pianeta, mettendo nella formula – r=arcsin (SA / SP) – il valore della distanza del pianeta che vogliamo considerare. Ecco i risultati ottenuti:
| Dal $pianeta$ |
il sole ha un diametro apparente di |
con magnitudine apparente |
| Mercurio | 1°22’26” | -28.80 |
| Venere | 43’57” | -27.43 |
| Terra | 31’58” | -26.74 |
| Marte | 19’17” | -25.64 |
| Giove | 6’08” | -23.16 |
| Saturno | 3’27” | -21.90 |
| Urano | 1’35” | -20.23 |
| Nettuno | 1’04” | -19.35 |
| Plutone | 1’01” | -19.25 |
Tramite il programma Celestia, ho creato altrettante immagini del Sole in prossimità del tramonto, da tutti i pianeti: è come aver realizzato una sorta di album fotografico andando proprio sulla superficie dei vari pianeti, da Mercurio a Plutone. Nel caso di Venere (immagine) in realtà la coltre delle nuvole che circonda il pianeta impedirebbe la visione del disco solare, ma concedetemi la licenza poetica, per poter effettuare il paragone con le altre “foto”.
Per la Terra (immagine) vediamo il Sole attraverso qualche nuvola, mentre nel caso di Saturno (immagine), ecco apparire sulla destra anche i fantastici anelli! Noterete subito che già da Giove (immagine) il Sole è molto piccolo (5 volte più piccolo che dalla Terra), per diventare un puntino comunque luminosissimo.
E’ notevole il fatto che il Sole mantiene una magnitudine apparente che va da -28 fino a poco meno di -20. Vuol dire che, sì, il Sole a grandissime distanze è un puntino, ma è un puntino di gran lunga più brillante di tutte le stelle visibili. Considerato che la Luna ha una magnitudine apparente media di -12.7 ed è in grado, al buio, di proiettare la nostra ombra, a maggior ragione la stessa cosa succede anche su Plutone: quando in un lontano futuro forse atterreremo su quel pianeta nano, proietteremo comunque l’ombra sul terreno!


Belle immagini! Ma alla fine dai primi quattro pianeti la differenza apparente non è grandissima. Quanto ci può entrare, poi, l’eventuale ‘effetto lente’ delle atmosfere?
Comunque c’è da dire che nemmeno su Mercurio il Sole è così tanto grande: il diametro apparente è un po’ più di 2 volte quello visto dalla Terra. Magari si poteva pensare di vedere un Sole enorme, ma così non è! 🙂
Invece dai pianeti giganti in poi il Sole è veramente piccolo, ma (come ho già sottolineato nell’articolo) è veramente luminoso!
Preparatevi invece a vedere i pianeti dai loro satelliti principali! 😉
Allora sì che Marte, Giove e Saturno saranno così grandi ed imponenti da essere proprio inquietanti!
Saturno soprattutto, con gli anelli che in un caso vanno dall’orizzonte fin oltre lo zenit! 😯 Pensate che spettacolo sarebbe osservarli con i propri occhi!
Dimenticavo…
L’effetto lente si ha soltanto quando il sole è vicinissimo all’orizzonte e solo se c’è l’atmosfera! Ed è funzione della composizione e dello spessore della stessa: quindi non si guadagna più di tanto…
Di atmosfera, tolte Venere e la Terra e un po’ Marte e Plutone, per il resto non se ne parla…
😎 😎 😎 Wow! e finalmente! Complimenti! Era diverso tempo che pensavo a questa cosa…..da Mercurio però immaginavo che il Sole incombesse interamente il cielo e invece….Nell’immagine della Terra mi sembra un pò più piccolo del reale, sicuri che non è stato invertito con Venere? Bellissimo anche da Plutone, ad osservarlo da laggiù ad occhi nudi verrebbe sicuramente una malinconia….Chissà un ipotetico osservatore su Proxima Centauri come lo vedrebbe?..
Attendo con impazienza il ‘capitolo’ pianeta visto dal suo satellite! 😯
E poi… chissà, magari… ipotizzare come si vede la Galassia da un immaginario pianeta di una stella del punto più lontano dell’alone esterno…
@moreno:
no! è tutto giusto: lo puoi vedere dal valore riportato in alto a destra (fornito da Celestia) per il diametro apparente: 0° 43′ 56.1″ per Venere, mentre abbiamo 0° 32′ 0.7″ per la Terra. 😉
Ho appena fatto un viaggetto a 4 anni luce dal Sole! Ho fotografato il Sole da Proxima Centauri!
Come vedi è di grandezza 0.39! Una stella qualunque…
😯 ahh, spettacolare la vista dalla stella più vicina!…cioè, no, anzi questa cosa fà pensare, il possente Sole una stellina nel cielo come milioni d’altre.. 😥
Buongiorno, le utlime 3 immagini utilizzano tutte lo stesso link alla stessa foto, con risultato che si vede solo quella di mercurio.
Saluti 🙂
Sergio
@Sergio
Ciao Sergio, se passi il mouse sopra la foto appaiono i pulsanti per scorrere la galleria, Next e Prev 😉
scusa Pierluigi,
ma in realtà (visto che non si considera l’effetto atmosfera, che poi sarebbe uguale da Giove a Nettuno) a me sembra che il Sole appaia più grande da Urano che da Saturno e da Giove piurttosto che da Marte. Vi è sicuramente un effettio 2alone”, ma non vedo perchè non ci sia anche su Saturno… Forse il prgramma potrebbe limitarsi a stampare il DISCO apparente e non una visione un po’ artistica… Che ne dici?
@enzo
Vediamo… quello che fa fede è senz’altro il valore “diametro apparente” in alto a sinistra, che diminuisce man mano che si va verso Plutone…
Celestia aggiunge un effetto glare, un alone, a tutti gli oggetti: forse disabilitandolo si otterrebbe una visione più realistica. Il fatto è che il diametro del sole è molto piccolo (cioè pochi pixel), almeno con il valore di FOV (Field Of View, angolo di visuale) che ho usato in ogni foto (31° e rotti)… Magari poi si potrebbe zoomare di un certo fattore in tutte le foto…
Ci posso provare e, se i risultati sono migliori, chiederò a Stefano di sostituire le “foto”… 😉
Immagini sostituite, ora la scala è molto più reale. Ho modificato anche i valori in tabella rispetto alle distanze riportate sulle nuove figure.
Ottimo lavoro Pier, grazie! 😉
… sì, hai fatto bene! 🙂
Ovviamente sia il valore del semidiametro che della magnitudine apparente cambiano istante per istante dato che sia la terra che i pianeti si spostano lungo la loro orbita: i valori indicati nelle foto erano quelli del momento in cui ho “scattato la foto” (mi piace dire così! sembra quasi di essere sul posto a fotografare!).
Per rendere ancora meglio l’idea della differente ampiezza del Sole, visto dai vari pianeti, ho realizzato un quadro comparativo: in questo caso balza subito agli occhi la grandezza del Sole visto da mercurio rispetto a quella da plutone!
Perfetto Pierluigi e Simone !!
Benissimo, ora con le nuove foto -chiare!- ed il quadro comparativo, ci si rende conto perfettamente di come ammireranno il Sole i futuri astronauti dai vari pianeti. Anche l’immagine da Proxima è bellissima….e chissà da Sirio, che noi vediamo così brillante, ma che non credo sia altrettanto, anzi forse da lassù manco lo notano il sole.. 😎 😆
@Moreno: che delusione!
il Sole da Sirio appare come una stellina ancora più insignificante, appena di magnitudine 1.93, poco più luminosa della Polare, all’interno della costellazione di Ercole! 😯
Invece da Proxima Centauri il Sole è nella costellazione di Cassiopea, 😯 che non è più una grande “W”, ma ha un lato in più!
(Pare che i Proximani conoscano Cassiopea come la grande “/\/\/” (“grfmlk” nella loro lingua, poverissima di vocali) del cielo! 😉 😆 😆 😆 )
😥 ..Gia, chi direbbe che attorno a quella stellina orbita un ancor più insignificante palla con 6 miliardi di creature… un ultima domanda, Professore, e poi basta che sennò si rischia di diventare noiosi 👿 : A che distanza massima il nostro Sole sarà ancora visibile in una notte serena -e stellata!- ad un ipotetico osservatore umano, ad occhio nudo naturalmente (non con l’equivalente dell’Hubble eh!!) ?? 5 o 600 anni luce, suppongo…
@Moreno:
facile facile! basta applicare una formuletta:
M=m+5-5*log(d)
dove “M” è la magnitudine assoluta (4.83 per il Sole), “m” la magnitudine visuale (6, è la tua richiesta!) e “d” è la distanza espressa in parsec (1 parsec=3.26 anni luce) con “log” il logaritmo in base 10.
Quindi, con facili passaggetti matematici si ottiene d=17.13 parsec=55.87 anni luce.
Quindi per riuscire ancora a vedere il Sole ad occhio nudo devi arrivare a circa 56 anni luce da qui… Castore ad esempio è a 51 anni luce e da lì il Sole è già di magnitudine 5.8. Non faccio la “foto” perchè è alquanto deludente… 😉
Secondo me in questi calcoli c’è qualcosa di sbagliato. Impossibile che da Mercurio si veda un sole grande quasi quanto quello che si vede sulla Terra. Da Saturno in poi, la dimensione del sole è la stessa, nonostante le distanze aumentino a dismisura.
Concordo con Andrea, ma solo dai pianeti gassosi in poi… Comunque teniamo conto del fatto che queste sono foto idealmente dal pianeta, ma in realtà non c’è la superficie come punto di riferimento e questo inganna i nostri occhi. Però da Saturno in poi la dimensione del sole non cambia, forse è un problema di risoluzione grafica, benché le distanze aumentino e tantissimo.
@andrea
mamma mia! rispondo dopo millenni! Scusami, ma non me ne sono mai accorto del tuo commento… 😳
Evidentemente i calcoli non sono sbagliati: è solo una questione di riferimenti.
Comunque anche quando ci sono riferimenti ben noti, l’occhio umano rimane ingannato lo stesso: hai mai fatto caso come la Luna Piena sembri molto più grande quando è vicina all’orizzonte?
Eppoi da Mercurio il Sole è decisamente più grande rispetto alla Terra!
Quello che fa fede è il diametro apparente segnalato nelle varie foto, che varia da pianeta a pianeta: da Giove in poi il Sole è così piccolo che si fa pure fatica a paragonarlo con le altre foto…
PS mi è venuta in mente un’ideuzza per la questione dei riferimenti… vediamo se ci riesco…
vi farò sapere!
Ma ho una curiosità, come mai nell’universo il sole non illumina, cioè a noi arrivano i raggi e quindi fa luce, ci sono tante foto fatte dallo spazio del nostro pianeta, come mai si vede la Terra illuminata e lo spazio è tutto buio?
@Michael: Semplicemente perché sulla Terra abbiamo l’atmosfera che diffonde e rifrange la luce del Sole, e quindi tutto il cielo ci appare luminoso (e blu, visto che è la lunghezza d’onda meglio diffusa).
Nello spazio, però, l’atmosfera non c’è e quindi la luce non può essere diffusa, e tutto ci appare nero.
Se poi vuoi sapere perché lo spazio ci appare nero, questo dipende dal paradosso di Olbers, leggi QUI.